高等数学-多元微积分-多元微分学-向量值函数和向量分析

一元向量值函数 \(f: D \\rightarrow \\mathbf{R}^{n}\)

一元向量值函数定义

定义 设数集 \(D\\subset R\),则称映射 \(f: D \\rightarrow \\mathbf{R}^{n}\) 为一元向量值函数, 通常记为\(\\boldsymbol{r}=\\boldsymbol{f}(t), t \\in D\) 其中数集 D 称为函数的定义域, , t称为自变量, \(\\boldsymbol{r}\) 称为因变量.

例子：空间解析几何的参数方程形式，就是向量值函数

空间曲线\(\\Gamma\)的参数方程就是一个一元向量值函数， \(\\left{\\begin{array}{l}x=\\varphi(t) \\ y=\\psi(t), \\quad t \\in\[\\alpha, \\beta\] \\ z=\\omega(t)\\end{array}\\right.\) 也可以写成向量形式： \(\\boldsymbol{r}=x \\boldsymbol{i}+y \\boldsymbol{j}+z \\boldsymbol{k}, \\quad \\boldsymbol{f}(t)=\\varphi(t) \\boldsymbol{i}+\\psi(t) \\boldsymbol{j}+\\omega(t) \\boldsymbol{k}\) 简记为向量方程： \(\\boldsymbol{r}=\\boldsymbol{f}(t), t \\in\[\\alpha, \\boldsymbol{\\beta}\]\)

一元向量值函数的极限

定义 2 设向量值函数 \(f(t)\) 在点 \(t\_{0}\) 的某一去心邻域内有定义,如果存在一 个常向量 \(\\boldsymbol{r}_{0},\) 对于任意给定的正数 \(\\varepsilon,\) 总存在正数 \(\\delta,\) 使得当 \(t\) 满足 \(0\<\\left|t-t_{0}\\right|\<\\delta\)时，对应的函数值 \(\\boldsymbol{f}(t)\) 都满足不等式\(\\left|\\boldsymbol{f}(t)-\\boldsymbol{r}_{0}\\right|\<\\varepsilon\), 那么,常向量 \(\\boldsymbol{r}_{0},\) 就叫做向量值函数 \(\\boldsymbol {f(t)}\) 当 \(t \\rightarrow t\_{0}\) 时的极限 \(,\) 记作\(\\lim _{t \\rightarrow t_{0}} \\boldsymbol f(t)=\\boldsymbol r\_{0} \\quad\) 或 \(\\quad \\boldsymbol{f}(t) \\rightarrow \\boldsymbol{r}_{0}, l \\rightarrow t_{0}\)

向量值函数 \(\\boldsymbol {f(t)}\) 当 \(t \\rightarrow t\_{0}\) 时极限存在的充分必要条件是：三个分量函数 \(f\_{1}(t), f\_{2}(t), f\_{3}(t)\) 当 \(t \\rightarrow t\_{0}\) 时的极限都存在。 即\(\\lim _{t \\rightarrow t_{0}} \\boldsymbol f(t)=\\left(\\lim _{t \\rightarrow t_{0}} f\_{1}(t), \\lim _{t \\rightarrow t_{0}} f\_{2}(t), \\lim _{t \\rightarrow t_{0}} f\_{3}(t)\\right)\)

一元向量值函数的连续性

向量值函数 \(\\boldsymbol {f(t)}\) 在\(t\_{0}\) 连续的充分必要条件是：三个分量函数 \(f\_{1}(t), f\_{2}(t), f\_{3}(t)\) 都在在\(t\_{0}\) 连续

一元向量值函数的导数或导向量

向量值函数 \(\\boldsymbol {f(t)}\) 在\(t\_{0}\)的某邻域内有定义， 如果\(\\lim _{\\Delta t \\rightarrow 0} \\frac{\\boldsymbol\\Delta r}{\\Delta t}=\\lim _{\\Delta t \\rightarrow 0} \\frac{\\boldsymbol f\\left(t_{0}+\\Delta t\\right)-\\boldsymbol f\\left(t_{0}\\right)}{\\Delta t}\)， 则称这个极限向量是此一元向量值函数的导数或导向量，记为\(\\boldsymbol{f}^{\\prime}\\left(t\_{0}\\right)\) 或 \(\\left.\\frac{\\mathrm{d} \\boldsymbol{r}}{\\mathrm{d} t}\\right|_{t=t_{0}}\)

向量值函数 \(\\boldsymbol {f(t)}\) 在\(t\_{0}\) 可导的充分必要条件是：三个分量函数 \(f\_{1}(t), f\_{2}(t), f\_{3}(t)\) 都在在\(t\_{0}\) 可导。 即\(\\boldsymbol{f}^{\\prime}\\left(t\_{0}\\right)=f\_{1}^{\\prime}\\left(t\_{0}\\right) \\boldsymbol{i}+f\_{2}^{\\prime}\\left(t\_{0}\\right) \\boldsymbol{j}+f\_{3}^{\\prime}\\left(t\_{0}\\right) \\boldsymbol{k}\)

一元向量值函数的导数运算法则，与数量函数的导数运算法则形式相同： \(\\frac{\\mathrm{d}}{\\mathrm{d} t} \\boldsymbol{C}=\\mathbf{0}\) \(\\frac{\\mathrm{d}}{\\mathrm{d} t}\[c \\boldsymbol{u}(t)\]=c \\boldsymbol{u}^{\\prime}(t)\) \(\\frac{\\mathrm{d}}{\\mathrm{d} t}\[\\boldsymbol{u}(t) \\pm \\boldsymbol{v}(t)\]=\\boldsymbol{u}^{\\prime}(t) \\pm \\boldsymbol{v}^{\\prime}(t)\) \(\\frac{\\mathrm{d}}{\\mathrm{d} t}\[\\varphi(t) \\boldsymbol{u}(t)\]=\\varphi^{\\prime}(t) \\boldsymbol{u}(t)+\\varphi(t) \\boldsymbol{u}^{\\prime}(t)\) \(\\frac{\\mathrm{d}}{\\mathrm{d} t}\[\\boldsymbol{u}(t) \\cdot \\boldsymbol{v}(t)\]=\\boldsymbol{u}^{\\prime}(t) \\cdot \\boldsymbol{v}(t)+\\boldsymbol{u}(t) \\cdot \\boldsymbol{v}^{\\prime}(t)\) \(\\frac{\\mathrm{d}}{\\mathrm{d} t}\[\\boldsymbol{u}(t) \\times \\boldsymbol{v}(t)\]=\\boldsymbol{u}^{\\prime}(t) \\times \\boldsymbol{v}(t)+\\boldsymbol{u}(t) \\times \\boldsymbol{v}^{\\prime}(t)\) \(\\frac{\\mathrm{d}}{\\mathrm{d} t} \\boldsymbol{u}\[\\varphi(t)\]=\\varphi^{\\prime}(t) \\boldsymbol{u}^{\\prime}\[\\varphi(t)\]\)

几何应用：在空间解析几何中的应用：空间曲线切向量、曲面法向量

向量值函数的几何意义

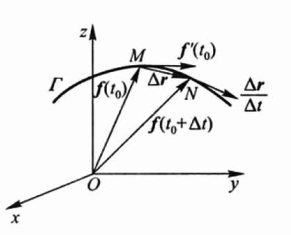
导向量 \(f^{\\prime}\\left(t\_{0}\\right)=\\lim \_{\\Delta t \\rightarrow 0} \\frac{\\Delta r}{\\Delta t}\) 是向量值函数 \(r=f(t)\) 的终端曲线 \(\\Gamma\) 在点 \(M\) 处的一个切向量,其指向与 \(t\) 的增长方向一致.

空间曲线的切线与法平面

空间曲线\(\\Gamma\)的参数方程就是一个一元向量值函数， \(\\left{\\begin{array}{l}x=\\varphi(t) \\ y=\\psi(t), \\quad t \\in\[\\alpha, \\beta\] \\ z=\\omega(t)\\end{array}\\right.\) 也可以写成向量形式： \(\\boldsymbol{r}=x \\boldsymbol{i}+y \\boldsymbol{j}+z \\boldsymbol{k}, \\quad \\boldsymbol{f}(t)=\\varphi(t) \\boldsymbol{i}+\\psi(t) \\boldsymbol{j}+\\omega(t) \\boldsymbol{k}\) 简记为向量方程： \(\\boldsymbol{r}=\\boldsymbol{f}(t), t \\in\[\\alpha, \\boldsymbol{\\beta}\]\)

由前面几何意义可知，导向量是向量值函数变化方向上的切向量。 则向量\(\\boldsymbol T=\\boldsymbol f^{\\prime}\\left(t\_{0}\\right)=\\left(\\varphi^{\\prime}\\left(t\_{0}\\right), \\psi^{\\prime}\\left(t\_{0}\\right), \\omega^{\\prime}\\left(t\_{0}\\right)\\right)\)就是曲线的一个切向量（要求三个导数不同时为0）（对参数求导组成得导向量） 曲线\(\\Gamma\)在点M处的切线方程\(\\frac{x-x\_{0}}{\\varphi^{\\prime}\\left(t\_{0}\\right)}=\\frac{y-y\_{0}}{\\psi^{\\prime}\\left(t\_{0}\\right)}=\\frac{z-z\_{0}}{\\omega^{\\prime}\\left(t\_{0}\\right)}\) 曲线\(\\Gamma\)在点M处的法平面方程\(\\varphi^{\\prime}\\left(t\_{0}\\right)\\left(x-x\_{0}\\right)+\\psi^{\\prime}\\left(t\_{0}\\right)\\left(y-y\_{0}\\right)+\\omega^{\\prime}\\left(t\_{0}\\right)\\left(z-z\_{0}\\right)=0\)

对于非参数方程形式的空间曲线，如（显函数形式）： \(\\left{\\begin{array}{l}y=\\varphi(x) \\ z=\\psi(x)\\end{array}\\right.\) 可以化为参数方程形式求解： \(\\left{\\begin{array}{l}x=x \\ y=\\varphi(x) \\ z=\\psi(x)\\end{array}\\right.\)

对于另一种非参数方程形式的空间曲线，如（隐函数方程组形式）： \(\\left{\\begin{array}{l}F(x, y, z)=0 \\ G(x, y, z)=0\\end{array}\\right.\) 可以（对方程组求自由元的导数+解线性方程组）的方式来求解,得曲线的切向量\((1,\\frac{dy}{dx}, \\frac{dz}{dx}) \\rightarrow …\) 看过下一节：曲面的切平面与法线后，可以将\(F(x,y,z)=0\)和\(G(x,y,z)=0\)看作两个曲面，分别求曲面的法向量\(\\boldsymbol n\_1, \\boldsymbol n\_2\)，空间曲线是两曲面的交线，空间曲线的切向量\(\\boldsymbol n = \\boldsymbol n\_1 \\times \\boldsymbol n\_2\)

曲面的切平面与法线

曲面方程\(F(x, y, z)=0\) 在曲面\(F(x, y, z)=0\)上，且过曲面上一点\(M(x\_0,y\_0,z\_0)\)的任意曲线，设曲线的参数方程为： \(\\left{\\begin{array}{l}x=\\varphi(t) \\ y=\\psi(t), \\quad t \\in\[\\alpha, \\beta\] \\ z=\\omega(t)\\end{array}\\right.\) 由上一节知，这条空间曲线的切线方程为\(\\frac{x-x\_{0}}{\\varphi^{\\prime}\\left(t\_{0}\\right)}=\\frac{y-y\_{0}}{\\psi^{\\prime}\\left(t\_{0}\\right)}=\\frac{z-z\_{0}}{\\omega^{\\prime}\\left(t\_{0}\\right)}\) \(F\[\\varphi(t), \\psi(t), \\omega(t)\] \\equiv 0\) F有连续偏导数的情况下，\(\\left.\\frac{\\mathrm{d}}{\\mathrm{d} t} F\[\\varphi(t), \\psi(t), \\omega(t)\]\\right|_{t=t_{0}}=0\) 即\(F\_{x}\\left(x\_{0}, y\_{0}, z\_{0}\\right) \\varphi^{\\prime}\\left(t\_{0}\\right)+F\_{y}\\left(x\_{0}, y\_{0}, z\_{0}\\right) \\psi^{\\prime}\\left(t\_{0}\\right)+F\_{z}\\left(x\_{0}, y\_{0}, z\_{0}\\right) \\omega^{\\prime}\\left(t\_{0}\\right)=0\) 引入向量\(\\boldsymbol{n}=\\left(\\boldsymbol{F}_{x}\\left(x_{0}, y\_{0}, z\_{0}\\right), F,\\left(x\_{0}, y\_{0}, z\_{0}\\right), F\_{z}\\left(x\_{0}, y\_{0}, z\_{0}\\right)\\right)\)，又有（见上一节）过曲面点\(M(x\_0,y\_0,z\_0)\)的任任意曲线切向量\(\\boldsymbol{T}=\\left(\\boldsymbol{\\varphi}^{\\prime}\\left(t\_{0}\\right), \\boldsymbol{\\psi}^{\\prime}\\left(t\_{0}\\right), \\boldsymbol{\\omega}^{\\prime}\\left(t\_{0}\\right)\\right)\) 即\(\\boldsymbol T \\cdot \\boldsymbol n = \\boldsymbol 0\) 这个与曲面上过点M的任意曲线切线都垂直的向量\(\\boldsymbol{n}=\\left(\\boldsymbol{F}_{x}\\left(x_{0}, y\_{0}, z\_{0}\\right), F,\\left(x\_{0}, y\_{0}, z\_{0}\\right), F\_{z}\\left(x\_{0}, y\_{0}, z\_{0}\\right)\\right)\)，就是空间曲面在\(M(x\_0,y\_0,z\_0)\)处的切平面的法向量，（对隐函数左侧求偏导组成的向量） 对应的切平面方程为\(F\_{x}\\left(x\_{0}, y\_{0}, z\_{0}\\right)\\left(x-x\_{0}\\right)+F\_{y}\\left(x\_{0}, y\_{0}, z\_{0}\\right)\\left(y-y\_{0}\\right)+F\_{z}\\left(x\_{0}, y\_{0}, z\_{0}\\right)\\left(z-z\_{0}\\right)=0\) 法线方程为\(\\frac{x-x\_{0}}{F\_{x}\\left(x\_{0}, y\_{0}, z\_{0}\\right)}=\\frac{y-y\_{0}}{F\_{y}\\left(x\_{0}, y\_{0}, z\_{0}\\right)}=\\frac{z-z\_{0}}{F\_{z}\\left(x\_{0}, y\_{0}, z\_{0}\\right)}\)

对于非隐函数形式的空间曲线，如（显函数形式）： \(z=f(x, y)\) 可以化为隐函数形式： \(F(x, y, z)=f(x, y)-z\) 对应的有： \(F\_{x}(x, y, z)=f\_{x}(x, y), F\_{y}(x, y, z)=f\_{y}(x, y), F\_{z}(x, y, z)=-1\) 则平面切点M处的法向量： \(\\boldsymbol{n}=\\left(f\_{x}\\left(x\_{0}, y\_{0}\\right), f\_{y}\\left(x\_{0}, y\_{0}\\right),-1\\right)\) 法向量单位化（化为方向余弦的形式：z轴向上）： 各分量分别为\(\\cos \\alpha=\\frac{-f\_{x}}{\\sqrt{1+f\_{x}^{2}+f\_{y}^{2}}}, \\cos \\beta=\\frac{-f\_{y}}{\\sqrt{1+f\_{x}^{2}+f\_{,}^{2}}}, \\cos \\gamma=\\frac{1}{\\sqrt{1+f\_{x}^{2}+f\_{\\gamma}^{2}}}\)

物理应用:速度与加速度

由前面几何意义可知，导向量是向量值函数变化方向上的切向量，进一步，可以赋予其物理意义。

设向量值函数\(\\boldsymbol{r}=\\boldsymbol{f}(t)\)是沿空间光滑曲线运动的质点 \(M\) 的位置向量，t代表时间 \(\\boldsymbol{v}(t)=\\frac{\\mathrm{d} \\boldsymbol{r}}{\\mathrm{d} t}\) 是质点 \(M\) 的速度向里,其方向与曲线相切 \(\\boldsymbol{a}(t)=\\frac{\\mathrm{d} v}{\\mathrm{d} t}=\\frac{\\mathrm{d}^{2} \\boldsymbol{r}}{\\mathrm{d} t^{2}}\) 是质点 \(M\) 的加速度向量.

多元向量值函数

方向导数（不是向量值函数）

方向导数不是多元向量值函数，但是它与梯度的定义有关，所以把它放到这里。

偏导数反应的是函数沿坐标轴方向的变化率。很多物理现象需要求解物理量沿特定方向的变化率，只靠偏导数数是显然不够的。有必要讨论函数沿特定方向的变化率。（给定方向，只求大小，是个标量）

以二元函数为例，给定\(P\_0(x\_0,y\_0)\)和附近的点\(P(x,y)\),当两点距离\(|PP\_0|\)足够小时， \(P\_0 P\)可以看作是直线段\(l\)， \(l\)上两点间距离\(|PP\_0|=t\)， \(l\)的方向向量\(\\boldsymbol e\_{l}=(\\cos \\alpha, \\cos \\beta)\) 参数方程：\(\\left{\\begin{array}{l}x=x\_{0}+t \\cos \\alpha \\ y=y\_{0}+t \\cos \\beta\\end{array}(t \\geqslant 0)\\right.\) 对于函数 \(f(x, y)\) 在 \(P\_{0}\\left(x\_{0}, y\_{0}\\right)\) 处沿方向 \(l\) 的变化率. 即函数增量与距离的比值，取极限，即\(\\left.\\frac{\\partial f}{\\partial l}\\right|_{\\left(x_{0}, y\_{0}\\right)}=\\lim _{t \\rightarrow 0^{\*}} \\frac{f\\left(x_{0}+t \\cos \\alpha, y\_{0}+t \\cos \\beta\\right)-f\\left(x\_{0}, y\_{0}\\right)}{t}\)，这里\(\\left.\\frac{\\partial f}{\\partial l}\\right|_{\\left(x_{0}, y\_{0}\\right)}\)称作函数的方向导数

对于方向取\(\\boldsymbol e\_l = \\boldsymbol i = (1,0)\),方向导数就是对x的偏导数\(\\left.\\frac{\\partial f}{\\partial l}\\right|_{\\left(x_{0}, y\_{0}\\right)} = f\_x|_{(x\_0,y\_0)}\) 对于方向取\(\\boldsymbol e\_l = \\boldsymbol j = (0,1)\),方向导数就是对y的偏导数\(\\left.\\frac{\\partial f}{\\partial l}\\right|_{\\left(x\_{0}, y\_{0}\\right)} = f\_y|\_{(x\_0,y\_0)}\)

定理 （方向导数存在的必要条件）如果函数 \(f(x, y)\) 在点 \(P\_{0}\\left(x\_{0}, y\_{0}\\right)\) 可微分,那么函数在该点沿任一方向\(l\) 的**方向导数存在,且有\(\\left.\\frac{\\partial f}{\\partial l}\\right|_{\\left(x_{0}, y\_{0}\\right)}=f\_{x}\\left(x\_{0}, y\_{0}\\right) \\cos \\alpha+f\_{y}\\left(x\_{0}, y\_{0}\\right) \\cos \\beta\)，**其中其中 \(\\cos \\alpha\) 和 \(\\cos \\beta\) 是方向 \(l\) 的方向余弦. 证明：由函数 \(f(x, y)\) 在点 \(P\_{0}\\left(x\_{0}, y\_{0}\\right)\) 可微分,得： \(\\begin{aligned} \& f\\left(x\_{0}+\\Delta x, y\_{0}+\\Delta y\\right)-f\\left(x\_{0}, y\_{0}\\right) =\& f\_{x}\\left(x\_{0}, y\_{0}\\right) \\Delta x+f\_{y}\\left(x\_{0}, y\_{0}\\right) \\Delta y+o(\\sqrt{(\\Delta x)^{2}+(\\Delta y)^{2}}) \\end{aligned}\) 又\(\\Delta x=t \\cos \\alpha, \\Delta y=t \\cos \\beta, \\sqrt{(\\Delta x)^{2}+(\\Delta y)^{2}}=t\) 得方向导数： \(\\begin{aligned} \\left.\\frac{\\partial f}{\\partial l}\\right|_{\\left(x_{0}, y\_{0}\\right)}\&= \\lim _{t \\rightarrow 0^{+}} \\frac{f\\left(x_{0}+t \\cos \\alpha, y\_{0}+t \\cos \\beta\\right)-f\\left(x\_{0}, y\_{0}\\right)}{t} \\\&= \\lim _{t \\rightarrow 0^{+}} \\frac{f_{x}\\left(x\_{0}, y\_{0}\\right) \\Delta x+f\_{y}\\left(x\_{0}, y\_{0}\\right) \\Delta y+o(\\sqrt{(\\Delta x)^{2}+(\\Delta y)^{2}})-f\\left(x\_{0}, y\_{0}\\right)}{t} \\ \&= f\_{x}\\left(x\_{0}, y\_{0}\\right) \\cos \\alpha+f\_{y}\\left(x\_{0}, y\_{0}\\right) \\cos \\beta \\end{aligned}\)

同理，对于三元函数 \(f(x, y, z)\) 来说, 它在空间一点 \(P\_{0}\\left(x\_{0}, y\_{0}, z\_{0}\\right)\) 沿方向 \(e\_{l}=(cos \\alpha, \\cos \\beta, \\cos \\gamma )\)的方向导数为 \(\\left.\\frac{\\partial f}{\\partial l}\\right|_{\\left(x_{0}, y\_{0}, z\_{0}\\right)}=\\lim _{t \\rightarrow 0^{\*}} \\frac{f\\left(x_{0}+t \\cos \\alpha, y\_{0}+t \\cos \\beta, z\_{0}+t \\cos \\gamma\\right)-f\\left(x\_{0}, y\_{0}, z\_{0}\\right)}{t}\) 同样可证，三元函数 \(f(x, y, z)\) 在空间一点 \(P\_{0}\\left(x\_{0}, y\_{0}, z\_{0}\\right)\) 可微，则该函数沿方向 \(\\boldsymbol e\_{i}=(\\cos \\alpha, \\cos \\beta, \\cos \\gamma)\) 的方向导数为\(\\left.\\frac{\\partial f}{\\partial l}\\right|_{\\left(x_{0}, y\_{0}, z\_{0}\\right)}=f\_{x}\\left(x\_{0}, y\_{0}, z\_{0}\\right) \\cos \\alpha+f\_{y}\\left(x\_{0}, y\_{0}, z\_{0}\\right) \\cos \\beta+f\_{z}\\left(x\_{0}, y\_{0}, z\_{0}\\right) \\cos \\gamma\)

梯度

二元函数梯度的定义

以二元函数为例，函数 \(f(x, y)\) 在点 \(P\_{0}\\left(x\_{0}, y\_{0}\\right)\) 可微分,那么函数在该点沿任一方向\(l\) 的**方向导数存在,且有$\left.\frac{\partial f}{\partial l}\right|{\left(x{0}, y_{0}\right)}=f_{x}\left(x_{0}, y_{0}\right) \cos \alpha+f_{y}\left(x_{0}, y_{0}\right) \cos \beta = (f_{x}\left(x_{0}, y_{0}\right) ,f_{,}\left(x_{0}, y_{0}\right) ) \cdot (\cos \alpha, \cos \beta) $，**其中其中 \(\\cos \\alpha\) 和 \(\\cos \\beta\) 是方向 \(l\) 的方向余弦，则\(\\boldsymbol e\_{l}=(\\cos \\alpha, \\cos \\beta)\)是单位方向向量

我们可以将**\((f\_{x}\\left(x\_{0}, y\_{0}\\right) ,f\_{,}\\left(x\_{0}, y\_{0}\\right) )\)向量（向量值函数），定义为梯度**： \(\\boldsymbol {grad} f\\left(x\_{0}, y\_{0}\\right)=\\nabla f\\left(x\_{0}, y\_{0}\\right)=f\_{x}\\left(x\_{0}, y\_{0}\\right) \\boldsymbol i+f\_{,}\\left(x\_{0}, y\_{0}\\right) \\boldsymbol j = (f\_{x}\\left(x\_{0}, y\_{0}\\right) ,f\_{,}\\left(x\_{0}, y\_{0}\\right) )\) 它是定义在多元函数上的向量值函数，\(D \\rightarrow \\mathbf{R}^{n}\) ，由标量函数\(f(x,y)\)经过\(\\nabla\)算子的操作，映射到向量空间。

那么，方向导数可以看作是梯度和单位方向向量的内积： \(\\begin{aligned}\\left.\\frac{\\partial f}{\\partial l}\\right|_{\\left(x_{0}, y\_{0}\\right)} \&=f\_{x}\\left(x\_{0}, y\_{0}\\right) \\cos \\alpha+f\_{y}\\left(x\_{0}, y\_{0}\\right) \\cos \\beta \\ \&=\\boldsymbol{grad} f\\left(x\_{0}, y\_{0}\\right) \\cdot \\boldsymbol e\_{i}=\\left|\\boldsymbol{grad} f\\left(x\_{0}, y\_{0}\\right)\\right| \\cos \\theta \\end{aligned}\) 其中\(\\theta\)是两个向量的夹角。

梯度方向是方向导数取最大值的方向，梯度的模就是方向导数的最大值。

\(\\begin{aligned}\\left.\\frac{\\partial f}{\\partial l}\\right|_{\\left(x_{0}, y\_{0}\\right)} \&=\\boldsymbol{grad} f\\left(x\_{0}, y\_{0}\\right) \\cdot \\boldsymbol e\_{i}=\\left|\\boldsymbol{grad} f\\left(x\_{0}, y\_{0}\\right)\\right| \\cos \\theta \\end{aligned}\)

• 当方向导数和梯度的方向相同时，即\(\\theta = 0\)时，方向导数最大，函数增加最快。 梯度方向是方向导数取最大值的方向，梯度的模就是方向导数的最大值。
• 同理，当方向导数和梯度的方向相反时，即\(\\theta = \\pi\)时，方向导数最小，函数减小最快。 梯度的反方向是方向导数取最小值的方向，梯度模的相反数就是方向导数的最小值。
• 同理，当方向导数和梯度的方向正交时，即\(\\theta = \\pi / 2\)时，方向导数为0，函数变化率为0。

二元函数等值线的法线方向是梯度方向

二元函数 \(z=f(x, y)\) 在几何上表示一个曲面，它和平面\(z=c\)截得的曲线叫做等值线。 二元函数的等值线\(\\left{\\begin{array}{l}z=f(x, y) \\ z=c\\end{array}\\right.\)有3个变量2个约束1个自由元， 用代入消元或隐函数方程组的方法可求\(\\frac{dy}{dx}= -\\frac{f\_x}{f\_y}\), 由前面向量值函数\(\\boldsymbol r = x \\boldsymbol i + y \\boldsymbol j + z \\boldsymbol k = (x,y,z)\)的导函数的几何意义可知，向量\((\\frac{dx}{dx}, \\frac{dy}{dx},\\frac{dz}{dx}) = (1, \\frac{dy}{dx},0)\)代表空间曲线的切向量，此切向量z分量为0，\(z=c\)平面上切向量分量\((\\frac{dx}{dx}, \\frac{dy}{dx}) = (1, \\frac{dy}{dx})\)，则**\(z=c\)平面上法向量为$(1,-\frac{dx}{dy})= (1, \frac{f_y}{f_x}) $， 单位化法向量: \(\\begin{aligned} \\boldsymbol n \&=\\frac{1}{\\sqrt{f\_{x}^{2}\\left(x\_{0}, y\_{0}\\right)+f\_{y}^{2}\\left(x\_{0}, y\_{0}\\right)}}\\left(f\_{x}\\left(x\_{0}, y\_{0}\\right), f\_{y}\\left(x\_{0}, y\_{0}\\right)\\right) \\ \&=\\frac{\\nabla f\\left(x\_{0}, y\_{0}\\right)}{\\left|\\nabla f\\left(x\_{0}, y\_{0}\\right)\\right|} \\end{aligned}\) 即二元函数等值线在\(z=c\)平面上的法线方向就是梯度方向**

三元函数梯度的定义

类似二元函数梯度（是个向量值函数）的定义，可以定义三元函数的梯度。

只要函数\(f(x,y,z)\)在空间区域D有连续偏导数，在空间中任意点\((x\_0,y\_0,z\_0)\)都可定义梯度

\(\\begin{aligned} \\operatorname{grad} f\\left(x\_{0}, y\_{0}, z\_{0}\\right) \&=\\nabla f\\left(x\_{0}, y\_{0}, z\_{0}\\right) \\ \&=f\_{x}\\left(x\_{0}, y\_{0}, z\_{0}\\right) \\boldsymbol{i}+f\_{,}\\left(x\_{0}, y\_{0}, z\_{0}\\right) \\boldsymbol{j}+f\_{i}\\left(x\_{0}, y\_{0}, z\_{0}\\right) \\boldsymbol{k} \\end{aligned}\)

其中\(\\nabla =\\frac{\\partial}{\\partial x} i+\\frac{\\partial}{\\partial y} j+\\frac{\\partial}{\\partial z} k\) 称为(三维的) 向量微分算子或 Nabla 算子 \(, \\nabla f=\\frac{\\partial f}{\\partial x} i+\\frac{\\partial f}{\\partial y} j+\\frac{\\partial f}{\\partial z} k\)

三元函数等值面的法线方向是梯度方向

曲面\(f(x, y, z)=c\)是函数\(f(x,y,z)\)的等值面，写成标准形式是\(F(x,y,z) = f(x,y,z) – c = 0\), 有3变量1约束2自由元，可求得\((F\_x,F\_y,F\_z) = (f\_x, f\_y, f\_z)\) 由前面的几何意义可知，对于空间曲面（等值面）上任意点\(M(x\_0,y\_0,z\_0)\)，向量\(\\left(\\boldsymbol{F}_{x}\\left(x_{0}, y\_{0}, z\_{0}\\right), F,\\left(x\_{0}, y\_{0}, z\_{0}\\right), F\_{z}\\left(x\_{0}, y\_{0}, z\_{0}\\right)\\right)\)，就是空间曲面（等值面）\(F(x, y, z)=0\)在\(M(x\_0,y\_0,z\_0)\)处的切平面的法向量， 单位化法向量： \(\\begin{aligned} \\boldsymbol n \&=\\frac{1}{\\sqrt{f\_{x}^{2}\\left(x\_{0}, y\_{0}, z\_{0}\\right)+f\_{y}^{2}\\left(x\_{0}, y\_{0}, z\_{0}\\right)+f\_{y}^{2}\\left(x\_{0}, y\_{0}, z\_{0}\\right)}}\\left(f\_{x}\\left(x\_{0}, y\_{0}, z\_{0}\\right), f\_{y}\\left(x\_{0}, y\_{0}, z\_{0}\\right)\\right) \\ \&=\\frac{\\nabla f\\left(x\_{0}, y\_{0}, z\_{0}\\right)}{\\left|\\nabla f\\left(x\_{0}, y\_{0}, z\_{0}\\right)\\right|} \\end{aligned}\)

标量场\(f: \\mathbf{R}^{m} \\rightarrow \\mathbf{R}\)

如果对于空间区域G内的任意一点M，都有一个确定的数量\(f(M)\)，那么称在这片区域G中确定了一个数量场（如温度场、密度场等）。 一个数量场可以用一个数量函数\(f(M)\)来确定。

矢量场\(f: \\mathbf{R}^{m} \\rightarrow \\mathbf{R}^{n}\)

如果对于空间区域G内的任意一点M，如果与M对应的是一个向量\(\\boldsymbol F(M)\),那么称在这片区域中确定了 一个矢量场/向量场。（如力场、速度场等） 一个向量场可用一个向量值函数\(\\boldsymbol F(M)\)来确定。

如果向量场\(\\boldsymbol F(M)\)恰好是某个数量函数\(f(M)\)的梯度，即\(\\boldsymbol F(M) = \\nabla f(M)\)，这样的向量场\(\\boldsymbol F(M)\)称为势场，对应数量函数\(f(M)\)称为势函数

例如：