Contents
- 1 线性代数总结
- 1.1 向量
- 1.2 线性方程组
- 1.3 特征值与特征向量
- 1.4 二次型
- 1.5 易混概念辨析
线性代数总结
根据同济线性代数第一版的序言,线性代数本是高等数学第13章,后来提出来单独成书。
线性代数分为6块内容:行列式、矩阵、向量与向量空间、方程组、特征值、二次型。 概念互相渗透,联系紧密。
行列式、矩阵、向量、方程组联系尤为紧密。 向量是研究方程组的解的过程中,提炼抽象出来的。(并提出了向量的相关无关、向量的秩、矩阵的秩的概念) 行列式和矩阵式求解方程组的过程中,提炼的工具。(消元的过程中,无法避免\(ad-bc\)的形式,将其定义为二阶行列式;系数与未知数的相乘并相加,系数提出来更简洁,就成了系数矩阵) 矩阵按列分块,就变成了向量。(解方程组的问题就变成了各列向量能否线性表示b的问题)
二次型的几何意义:空间解析几何的二次曲面。
线性代数的难点和重点:
| 两难一重 | ||
|---|---|---|
| 重点一 | 方程组 | 有无解?有几个解?如何求解以及参数处理 |
| 重点二 | 特征值、特征向量 | \(A\\alpha = \\lambda \\alpha\),矩阵相似,对角阵相似。综合性强 |
| 难点 | 向量 | 线性表示、相关无关、秩 |
线性代数的特点: 1)概念多,定理多,运算法则多,符号多(易混淆) 2)内容上纵横交错,知识前后联系紧密(需要编织知识网络,重视一题多解)(解法灵活多变) 3)逻辑推理要求高(尤其是证明)
向量
概念,运算
线性表示
问\(\\alpha\_1, \\alpha\_2 … \\alpha\_n\) 能否线性表示\(\\beta\),等于问一个非齐次方程组\((\\alpha\_1, \\alpha\_2 … \\alpha\_n)X=\\beta\) 有解没解的问题.
线性相关与无关
线性相关与无关定义
设\(\\alpha\_1, \\alpha\_2, … ,\\alpha\_n\) 为一组n维向量,如果存在一组不全为0的数\(k\_1, k\_2, … , k\_s\),使得\(k\_1 \\alpha\_1 + k\_2 \\alpha\_2 + … + k\_s \\alpha\_s = 0\) 成立,称向量组\(\\alpha\_1, \\alpha\_2, … , \\alpha\_s\) 线性相关; 如果上述等式仅当\(k\_1 = k\_2 = … = k\_s = 0\) 时成立,则称向量组\(\\alpha\_1, \\alpha\_2, … , \\alpha\_s\) 线性无关
注意这里(n和s的区别)
问\(\\alpha\_1, \\alpha\_2 … \\alpha\_n\) 是否线性相关,等于问一个齐次方程组\((\\alpha\_1, \\alpha\_2 … \\alpha\_n)X=0\) 有解没解(是否只有0解)的问题.
n维向量的向量组 \(\\alpha\_{1}, \\alpha\_{2} \\cdots \\alpha\_{m}\) 线性相关 \(\\Leftrightarrow\) \(\\exists\) 不全为0的 \(k\_{1} k\_{2} \\cdots k\_{m}\) , s.t. \(k\_1 \\alpha\_1 + k\_2 \\alpha\_2 + \\cdots + k\_m \\alpha\_m = 0\) \(\\Leftrightarrow\) \(\\exists\) 不全为0的 \(k\_{1} k\_{2} \\cdots k\_{m}\) , s.t. \(\\left\[\\alpha\_{1} \\alpha\_{2} \\cdots \\alpha\_{m}\\right\]\\left\[\\begin{array}{l}{k\_{1}} {k\_{2}} {k\_{m}}\\end{array}\\right\]=0\) \(\\leftrightarrow\) \(\\left\[\\alpha\_{1} \\alpha\_{2} \\cdots \\alpha\_{m}\\right\]\\left\[\\begin{array}{l}{x\_{1}} {x\_{2}} {x\_{m}}\\end{array}\\right\]=0\) 存在非0解 \(\\Leftrightarrow\) \(r\\left(\\alpha\_{1} \\alpha\_{2} \\cdots \\alpha\_{m}\\right)\<m\)
推论
-
n个n维向量\(\\alpha\_1, \\alpha\_2 … \\alpha\_n\) 相关 \(\\Leftrightarrow\) \(|\\alpha\_1, \\alpha\_2 … \\alpha\_n|=0\)
-
n+1个n维向量必线性相关
-
\(\\alpha\_1, \\alpha\_2 … \\alpha\_s\) 相关,则\(\\alpha\_1, \\alpha\_2 … \\alpha\_s … \\alpha\_{s+r}\) 必相关
i.e. 方程组有非0解,添加几个未知数之后仍有非0解
-
低维向量线性无关,那么添加维度(坐标)后的高维向量也无关
e.g.
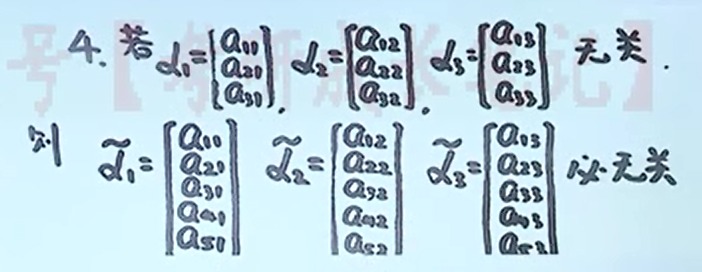
低维向量线性相关的几何意义
两个三维向量线性相关,表示向量共线(坐标成比例);
三个三维向量线性相关,表示共面(坐标成比例)
秩
极大线性无关组
设\(\\alpha\_1, \\alpha\_2, .. \\alpha\_s\) 是一个n维向量组,如果向量组中有r个向量线性无关,且向量的任意\(r+1\)个向量线性相关,则这r个线性无关的向量称为向量组\(\\alpha\_1, \\alpha\_2, .. \\alpha\_s\) 的极大线性无关组
向量组的秩
向量组\(\\alpha\_1, \\alpha\_2, .. \\alpha\_s\)的极大线性无关组中所含有向量的个数称为此向量组的秩,记作\(r(\\alpha\_1, \\alpha\_2, .. \\alpha\_s)\) 如果一个向量组仅含有零向量,则规定它的秩为0
[等价的向量组](# 等价矩阵)具有相同的秩
矩阵的秩
矩阵列向量组的秩,或者矩阵行向量组的秩,称为矩阵的秩
矩阵的秩也可以认为是不为0的余子式的最大阶数
矩阵与向量的秩的关联
\(r(A)=A的列秩=A的行秩\)
矩阵等价,秩相等.
向量组等价,秩相等;秩相等,向量组不一定等价.
矩阵秩公式
\(r(A^T)=r(A)\)
\(r(A+B)\\le r(A)+r(B)\)
\(r(kA)=r(A)\)
若A可逆,则 \(r(AB)=r(B), r(BA)=r(B)\)
\(r(AA^T)=r(A)\)
设A-mxn, B-nxs, 且\(AB=0\), 则\(r(A)+r(B) \\le n\)
\(\\left\[\\begin{matrix} A \& O O \& B\\end{matrix}\\right\]=r(A)+r(B)\)
定理:经过初等变换,矩阵的秩不变.
向量空间
运算封闭
若从某个非空数集中任选两个元素(同一元素可重复选出),选出的这两个元素通过某种(或几种)运算后的得数仍是该数集中的元素,那么,就说该集合对于这种(或几种)运算是封闭的
向量空间
设S是n维向量的非空集合,且S中向量对于加法和数乘运算是封闭的,则称S构成一向量空间
子空间
基底
若\(\\alpha\_1, \\alpha\_2, … \\alpha\_n\) 为向量空间S中的一个线性无关的向量组, 且S中任一向量可由\(\\alpha\_1, \\alpha\_2, … \\alpha\_n\) 线性表示, 称\(\\alpha\_1, \\alpha\_2, … \\alpha\_n\) 为向量空间中的一个基底
向量空间的维数
向量空间中,基底所含向量的个数,称为此向量空间的维数. 若\(\\alpha\_1, \\alpha\_2, … \\alpha\_n\) 为向量空间S的一个基底,则其维数为n, 称为n维向量空间, 记为\(R^n\)
坐标
基变换与坐标变换
内积
设向量:
\(\\alpha = \\left( \\begin{array} { c } { a \_ { 1 } } { a \_ { 2 } } { \\vdots } { a \_ { n } } \\end{array} \\right) , \\boldsymbol { \\beta } = \\left( \\begin{array} { c } { b \_ { 1 } } { b \_ { 2 } } { \\vdots } { b \_ { n } } \\end{array} \\right)\)
则\(\\alpha\) 与\(\\beta\) 内积为:
\(( \\boldsymbol { \\alpha } , \\boldsymbol { \\beta } ) = \\boldsymbol { \\alpha } ^ { \\mathrm { T } } \\boldsymbol { \\beta } = \\left( a \_ { 1 } , a \_ { 2 } , \\cdots , a \_ { n } \\right) \\left\[\\begin{array}{}{ b \_ { 1 } } { \\vdots } { b \_ { n } } \\end{array}\\right\] = a \_ { 1 } b \_ { 1 } + a \_ { 2 } b \_ { 2 } + \\cdots + a \_ { n } b \_ { n }\)
向量的长度: \(| \\boldsymbol { \\alpha } | = \\sqrt { a \_ { 1 } ^ { 2 } + a \_ { 2 } ^ { 2 } + \\cdots + a \_ { n } ^ { 2 } }\)
内积性质:
\(\\begin{array} { l } { ( \\boldsymbol { \\alpha } , \\boldsymbol { \\beta } ) = ( \\boldsymbol { \\beta } , \\boldsymbol { \\alpha } ) } { \\boldsymbol { \\alpha } = \\boldsymbol { 0 } \\Leftrightarrow ( \\boldsymbol { \\alpha } , \\boldsymbol { \\alpha } ) = 0 } { ( \\boldsymbol { \\alpha } , \\boldsymbol { \\beta } + \\boldsymbol { \\gamma } ) = ( \\boldsymbol { \\alpha } , \\boldsymbol { \\beta } ) + ( \\boldsymbol { \\alpha } , \\boldsymbol { \\gamma } ) } \\end{array}\)
正交
若两向量内积为0,则这两个向量正交 i.e. \(( \\boldsymbol { \\alpha } , \\boldsymbol { \\beta } ) = a \_ { 1 } b \_ { 1 } + a \_ { 2 } b \_ { 2 } + \\cdots + a \_ { n } b \_ { n } = 0\), 则 \(\\alpha\) 与 \(\\beta\)正交
施密特正交化方法
设\(\\alpha\_1, \\alpha\_2, …, \\alpha\_s\) 为\(R^s\) 中一组线性无关的向量
令:
\(\\begin{array} { l } { \\beta \_ { 1 } = \\alpha \_ { 1 } } { \\beta \_ { 2 } = \\alpha \_ { 2 } – \\frac { \\left( \\alpha \_ { 2 } , \\beta \_ { 1 } \\right) } { \\left( \\beta \_ { 1 } , \\beta \_ { 1 } \\right) } \\beta \_ { 1 } } { \\cdots } { \\beta \_ { s } = \\alpha \_ { s } – \\frac { \\left( \\alpha \_ { s } , \\beta \_ { 1 } \\right) } { \\left( \\beta \_ { 1 } , \\beta \_ { 1 } \\right) } \\beta \_ { 1 }\\cdots – \\frac { \\left( \\alpha \_ { s } , \\beta \_ { s – 1 } \\right) } { \\left( \\beta \_ { s – 1 } , \\beta \_ { s – 1 } \\right) } \\beta \_ { s – 1 } } \\end{array}\)
则 \(\\beta\_1, \\beta\_2, … \\beta\_s\) 相互正交
规范正交基
设 \(\\alpha\_1, \\alpha\_2, …, \\alpha\_n\) 为\(R^n\) 中一组基(底)
将其(施密特)正交化得 \(\\beta\_1, \\beta\_2, …, \\beta\_n\)
再将其单位化得\(\\boldsymbol { \\eta } \_ { 1 } = \\frac { \\boldsymbol { \\beta } \_ { 1 } } { \\left| \\boldsymbol { \\beta } \_ { 1 } \\right| }, \\eta \_ { 2 } = \\frac { \\beta \_ { 2 } } { \\left| \\beta \_ { 2 } \\right| } , \\cdots , \\eta \_ { n } = \\frac { \\beta \_ { n } } { \\left| \\beta \_ { n } \\right| }\)
则\(\\eta\_1, \\eta\_2, … , \\eta\_n\) 满足 \((\\eta\_i, \\eta\_j)=0, i \\neq j ; |\\eta\_i|=1, i=1,2, … , n\)
称\(\\eta\_1, \\eta\_2, … , \\eta\_n\) 为 \(R^n\) 中的一组规范正交基
正交矩阵
定义 设 \(\\eta\_1, \\eta\_2, … , \\eta\_n\) 为 \(R^n\) 中的一组规范正交基,令\(Q=\[\\eta\_1, \\eta\_2, … , \\eta\_n\]\) , 则Q满足\(Q^T Q = Q Q^T = E\) , 称为正交矩阵
如果n阶矩阵A满足\(A^T A = E\), 即(\(A^{-1} = A^T\)),那么称A为正交矩阵,简称正交阵
方阵A为正交矩阵\(\\Leftrightarrow\) A的列向量/行向量都是单位向量,且两两正交
正交矩阵性质:
\(\\begin{array} { l } { Q ^ { \\mathrm { T } } = Q ^ { – 1 } \\quad (Q^T Q=E)} { | Q | = \\pm 1 } \\end{array}\)
若\(Q\_1, Q\_2\) 为正交矩阵, 则 \(Q\_1, Q\_2\)仍为正交矩阵
线性方程组
线性方程组概念
线性方程组同解变形(矩阵行变换)
- 两个方程互换位置
- 非零常数乘到方程的两端
- 某方程的k被加到另一个方程上
齐次方程组\(Ax=0\)
无解,0解(唯一解),非零解
定理 齐次方程组\(A\_{m\\times n}x=0\) 有非零解 \(\\Leftrightarrow\) \(r(A)\<n\)
推论 当\(m\<n\) 时, \(Ax=0\) 必有非零解 (i.e. 方程组数小于未知数个数)
推论 当m=n时, \(Ax=0\) 有非零解 \(\\Leftrightarrow\) \(|A|=0\)
解的性质
if \(\\eta\) is solution of \(Ax=0\) , then \(k\\eta\) is solution, too.
if \(\\eta\_1, \\eta\_2\) is solution of \(Ax=0\), then \(k\_1\\eta\_1 + k\_2\\eta\_2\) is solution, too.
基础解系
齐次方程组的基础解系:方程组解向量的极大线性无关组
i.e.
- \(\\eta\_1, \\eta\_2, … \\eta\_t\) 是 \(Ax=0\) 的解
- \(\\eta\_1, \\eta\_2, … \\eta\_t\) 线性无关
- \(Ax=0\) 的任意一个解都可以由 \(\\eta\_1, \\eta\_2, … \\eta\_t\) 线性表出
齐次方程组解向量的极大线性无关组(基础解系)个数\(n-r(A)\)
定理 如果齐次方程组 \(Ax=b \\quad(II)\) 系数矩阵的秩 \(r(A)=r\<n\) , 则\(II\) 有 \(n-r\) 个线性无关的解,且 \(II\) 的任意一个解都可以由这\(n-r\) 个线性无关的解(基础解系)线性表出
定理 若 \(\\eta\_1, \\eta\_2, \\cdot\\cdot\\cdot \\eta\_t\) 是齐次方程组 \(II\) 的基础解系,则 \(II\) 的通解是是: \(k\_1 \\eta\_1 + k\_2 \\eta\_2 + \\cdot \\cdot \\cdot + k\_t \\eta\_t\), \(k\_1, k\_2, … , k\_t\) 是任意常数
相关无关
在向量组部分介绍过了: 向量的相关无关
非齐次方程组\(Ax=b\)
有解判定: 无解,唯一解, 无穷多解
定理 \(A x=b\) 有解 \(\\Leftrightarrow r(A)=r(\\overline A)\)
唯一解: \(r(A)=r(\\bar{A})=n\)
\(\\infty\) 解: \(r(A)=r(\\bar{A})\<n\)
无解: \(r(A)+1=r(\\bar{A})\)
解的形式
解的性质

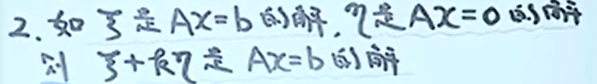
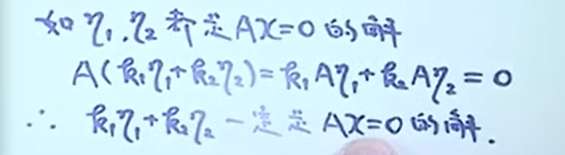
解的结构
定理 设\(\\alpha\) 是方程组\(Ax=b\) 的解, \(\\eta\_{1}, \\eta\_{2}, \\cdots, \\eta\_{t}\) 是导出组\(Ax=0\) 的基础解系,则方程组\(Ax=b\) 的通解为 \(\\alpha+k\_{1} \\eta\_{1}+k\_{2} \\eta\_{2} \\cdots+k\_{t} \\eta\_{t}\) , 其中 \(k\_{1} k\_{2} \\cdots k\_{t}\) 是任意常数
求解非齐次方程组做两件事:非齐次方程组求一个特解,求齐次方程组的基础解系,并用k衔接
公共解,同解
应用
- 相关无关\(\\Leftrightarrow\) 齐次方程组 \((\\alpha\_1, \\alpha\_2, \\cdot\\cdot\\cdot \\alpha\_s)x=0\)有非零解
- 线性无关\(\\Leftrightarrow\) 非齐次方程组 \((\\alpha\_1, \\alpha\_2, \\cdot\\cdot\\cdot \\alpha\_s)x=\\beta\) 有没有解
- \(AP=B\\neq P\)
- \(A \\alpha = \\lambda x\) 求x
特征值与特征向量
定义
\(A \\alpha=\\lambda \\alpha, \\alpha \\neq 0\), 注意特征向量不为0
说明(标准定义): 设A是n阶矩阵, \(\\alpha\)是n维非0列向量,满足: \(A \\alpha=\\lambda \\alpha\), 则称\(\\lambda\)是矩阵A的特征值, \(\\alpha\)是矩阵A属于特征值\(\\lambda\)的特征向量
性质
\(A \\alpha=\\lambda \\alpha, \\alpha \\neq 0 \\Rightarrow (A+k E) \\alpha=(\\lambda+k) \\alpha\)
\(A \\alpha=\\lambda \\alpha, \\alpha \\neq 0 \\Rightarrow A^{n} \\alpha=\\lambda^{n} \\alpha\)
\(|A|=\\prod \\lambda\)[^3](<矩阵特征值乘积等于矩阵行列式乘积的证明>)
\(A \\alpha=\\lambda \\alpha, \\alpha \\neq 0 \\Rightarrow A^{-1} \\alpha=\\frac{1}{\\lambda} \\alpha\)
若A可逆, \(\\lambda\) 是A的特征值, 则 \(\\frac{|A|}{\\lambda}\) 是\(A^\*\) 的特征值
性质总结:
设\(\\lambda\)是矩阵A的特征值,则矩阵\(kA, A^2, aA+bE, A^m, A^{-1}, A\*\) , 分别有特征值 \(k\\lambda, \\lambda^2, a\\lambda+b, \\lambda^m, \\frac{1}{\\lambda}, \\frac{|A|}{\\lambda}\)
设\(\\alpha\)是A对应\(\\lambda\)的特征向量,则\(\\alpha\)也是矩阵\(kA, A^2, aA+bE, A^m, A^{-1}, A\*\)对应特征值\(k\\lambda, \\lambda^2, a\\lambda+b, \\lambda^m, \\frac{1}{\\lambda}, \\frac{|A|}{\\lambda}\)的特征向量
求特征值与特征向量
利用定义与性质
利用定义式的变形得行列式求特征值(解行列式=0)
\(\\begin{array}{l}{ {\\left(\\lambda\_{i} E-A\\right) x=0} \\quad (x \\neq 0)\\ \\Rightarrow | \\lambda E-A |=0} \\ \\end{array}\)
再分别代入特征值\(\\lambda\_i\), 利用定义式的变形求特征向量(解齐次方程组)
\({\\left(\\lambda\_{i} E-A\\right) x=0} \\quad (x \\neq 0)\)
相似矩阵
定义:
\(A \\sim B:\) A, B都是n阶方阵, \(\\exists\) 可逆\(P, P^{-1} A P=B\) , 称A相似于B
\(A \\sim \\Lambda\)
矩阵相似的性质:
-
\(A \\sim A\)
-
\(A \\sim B \\Rightarrow B \\sim A\)
-
\(A \\sim B, B \\sim C \\Rightarrow A \\sim C\) (e.g. \(A \\sim \\Lambda, B \\sim \\Lambda \\Rightarrow A \\sim B\) 多用来证明)
-
\(A \\sim B \\Rightarrow A + kE \\sim B + kE\)
proof: \(P ^ { – 1 } ( A + k E ) P = P ^ { – 1 } A P + P ^ { – 1 } k E P = B + k E\)
-
\(A \\sim B \\Rightarrow A^n \\sim B^n\) proof: $A \sim B \Rightarrow P^{-1}AP=B \quad (两边平方) \Rightarrow (P{-1}AP)2=B^2 $, 数学归纳得原式
-
\(A \\sim B \\Rightarrow \\begin{equation} |\\lambda E-A|=|\\lambda E-B| \\Rightarrow \\lambda\_{A}=\\lambda\_{B} \\end{equation}\) proof: \(\\begin{aligned}|\\lambda E-B| \&=\\left|\\lambda E-P^{-1} A P\\right| \\ \&=\\left|P^{-1}(\\lambda E-A) P\\right| \\ \&=\\left|P^{-1}\\right|\\cdot|\\lambda E-A|\\cdot|P| \\ \&=|\\lambda E-A| \\end{aligned}\)
-
\(A \\sim B \\Rightarrow r(A)=r(B)\) proof: \(r(B)=r\\left(P^{-1} A P\\right) \=r(A P) \=r(A)\)
-
\(A \\sim B \\Rightarrow |A|=|B|\) proof: \(|B|=|P^{-1} A P| = |P^{-1} | \\cdot |A| \\cdot |P| = |A|\)
-
\(A \\sim B \\Rightarrow \\sum a\_{i i}=\\sum b\_{i i}\) (迹的和相等)
即:A相似B,{反身,传递,倍加E,n次}仍相似,相似则{特征值,秩,行列式,迹}相等。
性质推广
\(A \\sim B \\Rightarrow A^{-1} \\sim B^{-1}\)
证明:
\(\\begin{array}{l}{\\left(P^{-1} A P\\right)^{-1}=B^{-1}} \\ {P^{-1} A^{-1}\\left(P^{-1}\\right)^{-1}=B^{-1}} \\ {P^{-1} A^{-1} P=B^{-1}} \\ {\\therefore A^{-1} \\sim B^{-1}}\\end{array}\)
-
$A \sim B \Rightarrow A^T \sim B^T $
证明:
令\(\\left(P^{T} \\right)^{-1}=P\_1\)
则\(P\_1^{-1} A^T P\_1 = B^T\) -
\(A \\sim B \\Rightarrow A^\* \\sim B^\*\)
-
若\(\\mathbf{A} \\sim \\boldsymbol{B}, \\boldsymbol{C} \\sim \\boldsymbol{D}\), 则\(\\left\[\\begin{array}{ll}{A} \& {0} \\ {0} \& {C}\\end{array}\\right\] \\sim\\left\[\\begin{array}{ll}{B} \& {0} \\ {0} \& {D}\\end{array}\\right\]\)
-
若\(\\mathbf{A} \\sim B\),则\(f(\\boldsymbol{A}) \\sim f(\\boldsymbol{B}),|f(\\boldsymbol{A})|=|f(\\boldsymbol{B})|\),其中\(f(\\boldsymbol{A})\)为矩阵
相似对角化
相似对角化\(P^{-1} A P = \\Lambda\)的方法
设\(\\alpha \_ { 1 } , \\alpha \_ { 2 } , \\cdots , \\alpha \_ { n }\)为对应于特征值\(\\lambda\_i(i=1,2,…,n)\)的特征向量 \(\\begin{aligned} A \\left( \\alpha \_ { 1 } , \\alpha \_ { 2 } , \\cdots , \\alpha \_ { n } \\right) \& = \\left( A \\alpha \_ { 1 } , A \\alpha \_ { 2 } , \\cdots , A \\alpha \_ { n } \\right) \\ \& = \\left( \\lambda \_ { 1 } \\alpha \_ { 1 } , \\lambda \_ { 2 } \\alpha \_ { 2 } , \\cdots , \\lambda \_ { n } \\alpha \_ { n } \\right) \& =\\left\[ \\boldsymbol { a } \_ { 1 } , \\boldsymbol { \\alpha } \_ { 2 } , \\cdots , \\boldsymbol { \\alpha } \_ { n } \\right\] \\left\[ \\begin{array} { c c c c } { \\lambda \_ { 1 } } \\ { } \& { \\lambda \_ { 2 } } \\ { } \& { } \& { \\ddots } \\ { } \& { } \& { } \& { \\lambda \_ { n } } \\end{array} \\right\] \\end{aligned}\) 记\(P = \\left\[ \\alpha \_ { 1 } , \\alpha \_ { 2 } , \\cdots , \\alpha \_ { n } \\right\]\), 记\(\\boldsymbol { \\Lambda } = \\left\[ \\begin{array} { c c c c } { \\lambda \_ { 1 } } \\ { } \& { \\lambda \_ { 2 } } \\ { } \& { } \& { \\ddots } \\ { } \& { } \& { } \& { \\lambda \_ { n } } \\end{array} \\right\]\),
则\(P^{-1} A P = \\Lambda\)
性质
$A \sim \Lambda \Leftrightarrow $ A有n个线性无关的特征向量
\(\\lambda\)是k重特征值,则 \(\\lambda\)有k个无关的特征向量 \(\\Leftrightarrow A \\sim \\Lambda\)
A有n个不同的特征值$ \Rightarrow A \sim \Lambda$
A为对称矩阵 \(\\Rightarrow A \\sim \\Lambda\)
若\(P^{-1} A P = \\Lambda\), 则\(\\Lambda\)的主对角线上元素就是A的特征值,P的列向量就是A的特征向量[^2](<这也是构造可逆矩阵P和对角矩阵\(\\Lambda\)的方法>)
相似对角化可以用来求方阵的n次
实对称矩阵
如果有n阶矩阵A,其矩阵的元素都为实数,且矩阵A的转置等于其本身(\(a\_{ij}=a\_{ji}\))(i,j为元素的脚标),则称A为实对称矩阵(即\(A^T=A\)且元素为实数的矩阵)
特点
特征值必是实数
必与对角矩阵相似
可用正交矩阵相似对角化[^1]((一般的相似对角化是用特征向量可逆矩阵来实现相似对角化))
实对称矩阵用正交矩阵对角化的方法
- 求A的特征值\(\\lambda\_1, \\lambda\_2, … \\lambda\_n\)
- 求特征向量\(\\alpha\_1, \\alpha\_2 , … \\alpha\_n\)
- 改造特征向量为\(\\gamma\_1, \\gamma\_2, … , \\gamma\_n\)
- 如\(\\lambda\_i \\neq \\lambda\_j\), 只需单位化
- 如\(\\lambda\_i = \\lambda\_j\)
- 若\((\\alpha\_i, \\alpha\_j) = 0\), 只需单位化
- 若\(\\alpha\_i, \\alpha\_j) \\neq 0\), 施密特正交化,单位化
- 构造正交矩阵\(Q=(\\gamma\_1, \\gamma\_2, … , \\gamma\_n)\)
- 得\(Q^{-1} A Q = \\Lambda = \\left\[ \\begin{array} { c c c c } { \\lambda \_ { 1 } } \& { 0 } \& { \\cdots } \& { 0 } \\ { 0 } \& { \\lambda \_ { 2 } } \& { \\cdots } \& { 0 } \\ { \\vdots } \& { \\vdots } \& { \\vdots } \& { \\vdots } \\ { 0 } \& { 0 } \& { \\cdots } \& { \\lambda \_ { n } } \\end{array} \\right\]\)
二次型
概念、定理
二次型及其矩阵表示
设一个多元函数,其每一项都是二次的,这样的多元函数,称作二次型;任何一个二次型都可以用矩阵的乘法描写出来。
二次型矩阵化
n元二次型
\(f(x\_1, x\_2,…,x\_n) = \\Sigma{C\_{ii} x\_i x\_i} + \\Sigma{C\_{ij} x\_i x\_j} \= \[x\_1, x\_2, … , x\_n\] A \[x\_1, x\_2, … , x\_n\]^T \= x^T A x\) 其中A为一个对称矩阵,有 \(A(i,i) = C\_{ii}, A(i,j) = A(j,i) = C\_{ij}/2\)
函数f的平方项\(C\_{ii} x\_i x\_i\)系数依次填入对称矩阵P的对角线,函数f的混合项\(C\_{ij} x\_i x\_j\)系数除以2,分别填入矩阵A对应位置
这里的矩阵A称为二次型的矩阵
i.e. 一个三元二次型: \(\\begin{aligned} f\\left(x\_{1}, x\_{2}, x\_{3}\\right)=\& x\_{1}^{2}+5 x\_{2}^{2}+5 x\_{3}^{2}+2 x\_{1} x\_{2}-6 x\_{2} x\_{3} \\ \&=\\left\[x\_{1} x\_{2} x\_{3}\\right\]\\left\[\\begin{array}{ccc}{1} \& {1} \& {0} \\ {1} \& {5} \& {-3} \\ {0} \& {-3} \& {5}\\end{array}\\right\]\\left\[\\begin{array}{c}{x\_{1}} \\ {x\_{2}} \\ {x\_{3}}\\end{array}\\right\] \\end{aligned}\)
标准型
只有平方项,没有混合项的二次型
则标准型对应的矩阵是个对角矩阵
规范型
平方项系数只能为0,+1,-1的标准型
惯性指数
正惯性指数: 标准型中正的二次项个数
负惯性指数: 标准型中负的二次项个数
二次型的秩
\(r(f)=r(A)\)
坐标变换
以3元坐标为例:
\(\\left{\\begin{array}{l}{x\_{1}=c\_{11} y\_{1}+c\_{12} y\_{1}+c\_{13} y\_{3}} \\ {x\_{2}=c\_{21} y\_{1}+c\_{22} y\_{2}+c\_{23} y\_{3}} \\ {x\_{3}=c\_{31} y\_{1}+c\_{32} y\_{2}+c\_{33} y\_{3}}\\end{array} \\quad|C| \\neq 0\\right.\)
\(\\left\[\\begin{array}{l}{x\_{1}} \\ {x\_{2}} \\ {x\_{3}}\\end{array}\\right\]=\\left\[\\begin{array}{lll}{C\_{11}} \& {C\_{12}} \& {C\_{13}} \\ {C\_{21}} \& {C\_{22}} \& {C\_{23}} \\ {C\_{31}} \& {C\_{32}} \& {C\_{33}}\\end{array}\\right\]\\left\[\\begin{array}{l}{y\_{1}} \\ {y\_{2}} \\ {y\_{3}}\\end{array}\\right\]\)
那么通过坐标变换 \(x=Cy\),把坐标x用矩阵C变换为了y的坐标,这里要求C可逆
对二次型做坐标变换: \(\\left{ \\begin{array} { l } { f ( x ) = x ^ { T } A x } \\ { x = C y , | C | \\neq 0 } \\end{array} \\right.\) \(\\Rightarrow \\begin{aligned} g ( y ) = f \\left( C \_ { y } \\right) \& = \\left( C y \\right) ^ { T } A \\left( C y \\right) \& = y ^ { T } C ^ { T } A C y \& = y ^ { T } B y \\end{aligned}\) 其中\(B=C^T A C\)
矩阵合同
由对二次型的[坐标变换](# 坐标变换)可知,坐标变换${ x = C y , | C | \neq 0 } \(时, 二次型的矩阵A也变为B,并满足\)B=C^T A C$
定义
如果\(C^{T} A C=B\), 其中C是可逆矩阵,称矩阵A和B合同,记\(A \\simeq B\)
$A \simeq B \Leftrightarrow $ $x^T A x $ 与 \(x^T B x\) 正负惯性指数相同
性质
\(A \\simeq A\)
如果\(A \\simeq B\), 则\(B \\simeq A\)
如果\(A \\simeq B, B \\simeq C\),则\(A \\simeq C\)
任一实对称矩阵必合同于一个对角矩阵
定理 $x^T A x $ 经坐标变换\(x=Cy\), 有\(x^T A x = y^T B y\), 其中\(C^T A C = B\)
即二次型经坐标变换,二次型的矩阵变换为它的合同矩阵
定理 对任意\(x^T A x\), 都存在坐标变换\(x=Cy\),使得\(f=y^T \\Lambda y\)
即任意二次型都可以找到坐标变换,化为标准型
定理 (惯性定理) 对于一个二次型\(x^T A x\),经坐标变换化为标准型,其正惯性指数和负惯性指数都是唯一确定的
二次型变换为标准型的方法是不唯一的,即可能化为不同的标准型。但是这些标准型的正惯性指数和负惯性指数都是唯一确定的。
二次型变换为标准型
配方法
正交变换法
- 求特征值\(\\lambda\_1, \\lambda\_2, … , \\lambda\_n\)
- 求特征向量\(\\alpha\_1, \\alpha\_2, … , \\alpha\_n\)
- 改造特征向量(正交化,单位化)为\(\\gamma\_1, \\gamma\_2, … , \\gamma\_n\)
- 特征值不同,特征向量已正交,只需单位化
- 特征值有重根
- 该特征值的多个特征向量正交,只需单位化
- 该特征值的多个特征向量不正交,施密特正交化,并单位化
- 拼称正交矩阵\(Q=(\\gamma\_1, \\gamma\_2, …, \\gamma\_n)\)
- 令\(x=Qy\), 得\(x^T A x = y^T \\Lambda y, \\Lambda = \\left\[ \\begin{array} { c c c c } { \\lambda \_ { 1 } } \& { 0 } \& { \\cdots } \& { 0 } \\ { 0 } \& { \\lambda \_ { 2 } } \& { \\cdots } \& { 0 } \\ { \\vdots } \& { \\vdots } \& { \\vdots } \& { \\vdots } \\ { 0 } \& { 0 } \& { \\cdots } \& { \\lambda \_ { n } } \\end{array} \\right\]\)
简证:正交矩阵Q有\(Q^T = Q^{-1}\)的性质,结合[相似对角化](# 相似对角化)的证明过程,可知以上正交变换法是正确的
正定二次型
正定二次型定义
\(\\forall x = (x\_1, x\_2, … , x\_n)^T \\neq 0\),恒有\(f(x\_1, x\_2, … , x\_n) = x^T A x \> 0\), 则称f为正定二次型,A为正定矩阵
性质
合同变换不改变二次型的正定性
\(x^T A x\)正定二次型 \(\\Leftrightarrow\) 正惯性指数p=n \(\\Leftrightarrow\) \(A \\simeq E \\quad (i.e. \\exists |C| \\neq 0, C^T A C = E)\) \(\\Leftrightarrow\) A的特征值全大于0 \(\\Leftrightarrow\) A的顺序主子式全大于0 \(\\Leftrightarrow\) 存在可逆矩阵P,使\(A = P^T P\) \(\\Leftrightarrow\) 存在正交矩阵Q,使\(\\boldsymbol{Q}^{\\mathrm{T}} \\boldsymbol{A Q}=\\boldsymbol{Q}^{-1} \\mathrm{AQ}=\\left\[\\begin{array}{ccc}{\\lambda\_{1}} \& {} \& {} \\ {} \& {\\lambda\_{2}} \& {} \\ {} \& {} \& {\\ddots} \& {} \\ {} \& {} \& {} \& {\\lambda\_{n}}\\end{array}\\right\], \\lambda\_{i}\>0(i=1,2, \\cdots, n)\)
若A为正定矩阵,则\(k \\mathbf{A}(k\>0), \\mathbf{A}^{\\mathrm{T}}, \\mathbf{A}^{-1}, \\mathbf{A}^{\*}\)也是正定矩阵[^4](A正定,证明\(A^{-1}\)正定) 若A为正定矩阵,则\(|A|\>0\),从而A可逆 若A为正定矩阵,则A的主对角线上元素\(a\_{i i}\>0, i=1,2, \\cdots, n\)
- \((A^{-1})^T = (A^T)^{-1} \\overset{A \\text{正定}}{=} A^{-1}\) 所以\(A^{-1}\)是对称矩阵
- 设\(\\lambda\)是\(A^{-1}\)的特征值, \(\\alpha\)是对应的特征向量 \(\\therefore A^{-1} \\alpha = \\lambda \\alpha\) \(\\because\) A正定,其特征孩子全大于0 \(\\therefore\) A的特征值\(\\frac{1}{\\lambda} \> 0\) \(\\therefore \\lambda \> 0\) \(\\therefore A^{-1}\)正定
易混概念辨析
矩阵等价,合同,相似
矩阵等价 : 对同型矩阵A、B,存在可逆阵P和Q,使得B=PAQ 充要条件:A和B的秩相等 理解: 初等变换(行/列变换), 不改变矩阵的秩,变换前后的矩阵等价
[矩阵合同](# 矩阵合同): 对同型方阵A、B,存在可逆阵P, 使得\(B=P^T A P\)
[矩阵相似](# 相似矩阵): 对同型方阵A、B,存在可逆阵P, 使得\(B=P^{-1}AP, \\quad B=P^{-1}AP\)
三者关系:
等价(只有秩相同)–>合同(秩和正负惯性指数相同)–>相似(秩,正负惯性指数,特征值均相同),矩阵亲密关系的一步步深化。
相似矩阵必为等价矩阵,但等价矩阵未必为相似矩阵 PQ=EPQ=E 的等价矩阵是相似矩阵 合同矩阵必为等价矩阵,等价矩阵未必为合同矩阵 正惯性指数相同的等价矩阵是合同矩阵 合同矩阵未必是相似矩阵 相似矩阵未必合同 正交相似矩阵必为合同矩阵,正交合同矩阵必为相似矩阵 如果A与B都是n阶实对称矩阵,且有相同的特征根.则A与B既相似又合同
方程组系数矩阵的秩,方程组解的秩
对于齐次方程组: \[
\\left{ \\begin{array} { l } { x \_ { 1 } – x \_ { 2 } + 2 x \_ { 3 } – 3 x \_ { 4 } = 0 } \\
{ 2 x \_ { 1 } – 2 x \_ { 2 } + 4 x \_ { 3 } + 6 x \_ { 4 } = 0 } \\end{array} \\right.
\] 其系数矩阵: \[
A=\\left\[\\begin{array}{rrrr}{1} \& {-1} \& {2} \& {-3} \\
{2} \& {-2} \& {4} \& {6}\\end{array}\\right\]\\rightarrow\\left\[\\begin{array}{rrrr}{1} \& {-1} \& {2} \& {-3} \\
{0} \& {0} \& {0} \& {12}\\end{array}\\right\]\\rightarrow\\left\[\\begin{array}{rrrr}{1} \& {-1} \& {2} \& {0} \\
{0} \& {0} \& {0} \& {1}\\end{array}\\right\]
\]
系数矩阵A的秩:\(r(A)=2\)
方程组系数矩阵A(或者A的列向量)的极大线性无关组: \(\\left\[\\begin{array}{l}{1} {2}\\end{array}\\right\],\\left\[\\begin{array}{r}{-3} {6}\\end{array}\\right\]\)
方程组极大线性无关组(基础解系)个数,即解的秩: \(n-r(A)=4-2=2\) \(\\begin{array}{l}{x\_{2}=1, x\_{3}=0} \\quad \\rightarrow {\\eta\_{1}=(1,1,0,0)^{T}} {x\_{2}=0, x\_{3}=1} \\quad \\rightarrow {\\eta\_{2}=(-2,0,1,0)^{T}}\\end{array}\)
方程组解向量的极大线性无关组(基础解系): \(\\left\[\\begin{array}{c}{1} {1} {0} {0}\\end{array}\\right\],\\left\[\\begin{array}{c}{-2} {0} {1} {0}\\end{array}\\right\]\)
秩,极大线性无关组个数,系数矩阵的秩,方程组的基础解系
线性无关(组):仅当\(k\_1 = k\_2 = … = k\_s = 0\) 时, 得\(k\_1 \\alpha\_1 + k\_2 \\alpha\_2 + … + k\_s \\alpha\_s = 0\) 成立,称向量组\(\\alpha\_1, \\alpha\_2, … , \\alpha\_s\) 线性无关
[极大线性无关组](# 极大线性无关组):向量组中有r个向量线性无关,且向量的任意\(r+1\)个向量线性相关,这r个线性无关的向量称为向量组的极大线性无关组
[秩](# 秩): 极大线性无关组中向量的个数
(方程组\(Ax=\\beta\)的)系数矩阵:A
(方程组\(Ax=\\beta\)的)增广矩阵:\((A|\\beta)\)
(方程组\(Ax=\\beta\)的)基础解系:方程组解空间的极大线性无关组
(方程组\(Ax=\\beta\)的)系数矩阵的秩:\(r(A)\)
(方程组\(Ax=\\beta\)的)基础解系的秩:\(n-r(A)\)
行列式同等变形, 矩阵行/列变换, 方程组同解变形
说明
(行/列)倍乘: 非零元素乘以某一行(列)
(行/列)倍加: 非零元素乘以某一行(列),加到另一行(列)上
(行/列)互换: 某一行(列)与另一行(列)位置互换
区别
矩阵行/列变换
不是同等变形(变形前后不是“=”关系)
变换规则:倍乘, 倍加, 互换
有些情况只能行变换 e.g. 增广矩阵变换\((A|\\beta) \\rightarrow (E|\\beta')\), 矩阵求逆\((A|E)\\rightarrow (E|A^{-1})\)
行列式同等变形
是同等变形
变形规则: (行/列)倍乘, (行/列)倍加, (行/列)互换(互换位置行列式取反)
方程组同解变形
是同等变形
变形规则: 行倍乘, 行倍加, 行互换
[极大线性无关组]:
发表回复