线性代数-向量组的线性相关性习题
向量组与矩阵
例1

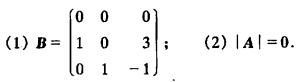
(1)由于AP=PB, 即: \(A(x,Ax,A^2x)=(Ax,A^2x,A^3x)=(Ax,A^2x,3Ax-2A^2x)=(x,Ax,A^2x)\\left\[\\begin{array}{c} 0\& 0\& 0 1\& 0\& 3 0\& 1\& -2\\end{array}\\right\]\) , 从而: \(AP=P \\left\[\\begin{array}{c} 0\& 0\& 0 1\& 0\& 3 0\& 1\& -2\\end{array}\\right\]\) , 所以: \(B= \\left\[\\begin{array}{c} 0\& 0\& 0 1\& 0\& 3 0\& 1\& -2\\end{array}\\right\]\)
- \(|A|=|PAP^{-1}| \=|P|\\cdot |B| \\cdot |P^{-1}| \=|P|\\cdot |B| \\cdot |P|^{-1} \=|B| \=0\)
向量组的线性表示
向量b可由向量组A线性表示的证明
例1

- 要证: \(a\_{1}\) 能由 \(a\_{2}, a\_{3}\) 线性表示\(\\Leftrightarrow\) 即证\(a\_1 = (a\_2, a\_3) \\left(\\begin{array}{c} k\_1 \\ k\_2 \\end{array}\\right)\)有解 \(\\Leftrightarrow\) 即证\(R(a\_2, a\_3) = R(a\_2, a\_3, a\_1)\) 由\(R\\left(a\_{2}, a\_{3}, a\_{4}\\right)=3\)得,\(a\_{2}, a\_{3}, a\_{4}\)线性无关,则\(a\_{2}, a\_{3}\)线性无关,则\(R(a\_{2}, a\_{3})=2\) 又\(R\\left(a\_{1}, a\_{2}, a\_{3}\\right)=2\) 则\(R\\left(a\_{1}, a\_{2}, a\_{3}\\right)=R(a\_2, a\_3)\),则\(a\_1 = (a\_2, a\_3) \\left(\\begin{array}{c} k\_1 \\ k\_2 \\end{array}\\right)\)有解,则\(a\_{1}\) 能由 \(a\_{2}, a\_{3}\) 线性表示
(2)要证\(a\_{4}\) 不能由 \(a\_{1}, a\_{2}, a\_{3}\) 线性表示\(\\Leftrightarrow\) 即证\(a\_4 = (a\_1,a\_2, a\_3) \\left(\\begin{array}{c} x\_1 \\ x\_2 \\x\_3 \\end{array}\\right)\)无解 \(\\Leftrightarrow\) 即证\(R(a\_1,a\_2, a\_3) \< R(a\_1,a\_2, a\_3,a\_4 )\)
\(R(a\_1,a\_2, a\_3,a\_4 ) \\ge R\\left(a\_{2}, a\_{3}, a\_{4}\\right)=3 \> R\\left(a\_{1}, a\_{2}, a\_{3}\\right)=2\) 则\(a\_4 = (a\_1,a\_2, a\_3) \\left(\\begin{array}{c} x\_1 \\ x\_2 \\x\_3 \\end{array}\\right)\)无解, 则\(a\_{4}\) 不能由 \(a\_{1}, a\_{2}, a\_{3}\) 线性表示
例2


解:由题意知,λbai1(a1+b)=λ2(a2+b) 其中,λdu1≠λzhi2,且两数不全为0
于是dao有:(λ2-λ1)b=λ1a1-λ2a2
b=a1λ1/(λ2-λ1)-a2λ2/(λ2-λ1)
令λ1/(λ2-λ1)=c,则:
λ2/(λ2-λ1)=1+c,(c∈R)
于是,b=ca1-(1+c)a2
例3

证法一: 先证必要性(前推后),因为任意n+1个n维向量必线性相关。所以任意向量b与a1…an相关。存在不完全为0的n+1个数k1…kn,kn+1.使得k1a1+…knan+kn+1*b=0;若kn+1=0,a1…an相关,矛盾,所以kn+1不等于0.即b可以被a1…an线性表出。即表示为a1…an的线性组合。 充分性,n维单位向量e1…en可以被a1…an线性表出。a1…an也可以被e1…en线性表出。所以他们等价。所以a1…an的秩为n。所以a1…an线性无关。 证毕。
证法二: 必要性: a1,a2,…an线性无关 => |a1,a2,…an| ≠ 0 => 对任一n维向量b, (a1,a2,…an)X = b 有解 => 任一n维向量b都可被a1,a2,…an线性表示 充分性: 因为任一n维向量都可被a1,a2,…an线性表示 所以n维基本向量组ε1,ε2,…,εn可由a1,a2,…an线性表示 所以 n = r(ε1,ε2,…,εn) <= r(a1,a2,…an). 所以 a1,a2,…an 线性无关.
例4 存在类的证明一般用反证法
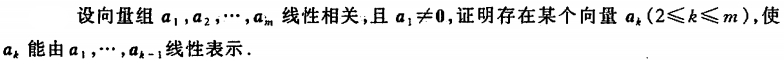
解: 设对任一\(a\_k (2\\le k \\le m)\)都不能由\(a\_1, a\_2, … , a\_{k-1}\)线性表示, 则\((a\_1, a\_2, … , a\_{k-1})x = a\_k\)无解, 则\(r(a\_1, a\_2, … , a\_{k-1}) \< r(a\_1, a\_2, … , a\_{k-1}, a\_k)\) 则\(1=r(a\_1) \< r(a\_1, a\_2)\<…\<r(a\_1, a\_2, … , a\_{k})\) 则\(r(a\_1, a\_2, … , a\_{k}) = k\) 取\(k=m\),得\(r(a\_1, a\_2, … , a\_{m}) = m\), 即有\(a\_{1}, a\_{2}, \\cdots, a\_{m}\)线性无关,这与已知矛盾。 所有假设不成立,所以存在某个向量 \(a\_{k}(2 \\leqslant k \\leqslant m)\),使\(a\_{k}\) 能由 \(a\_{1}, \\cdots, a\_{k-1}\) 线性表示。
向量组B可由向量组A线性表示的证明
例1

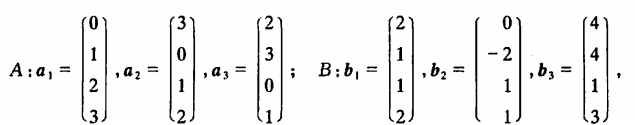

注意到:
B组能由A线性表示\(\\Leftrightarrow\)B=AX有解\(\\Leftrightarrow\) \(r(A)=r(A,B)\)
A组不能由B线性表示\(\\Leftrightarrow\)A=BX无解\(\\Leftrightarrow\) \(r(B)\<r(A,B)\)
向量组B与向量组A等价的证明
例1

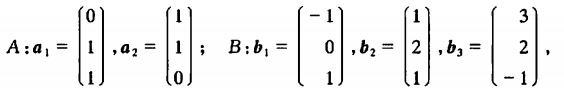
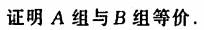
注意到:
向量组B与向量组A等价\(\\Leftrightarrow\) \(r(A) = r(B) = r(A,B)\)
例2
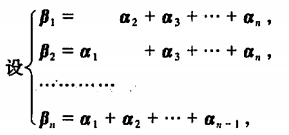
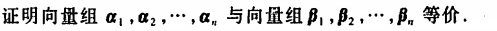
解: 根据已知:向量组\(\\beta\_1, \\beta\_2, …, \\beta\_n\)可以由向量组\(\\alpha\_1, \\alpha\_2, … \\alpha\_n\)表示,可以写成矩阵方程: \((\\beta\_1, \\beta\_2, …, \\beta\_n) = (\\alpha\_1, \\alpha\_2, … \\alpha\_n)\\left\[\\begin{array}{c}0 \& 1 \&\\cdots \&1 \\1 \& 0 \& \\cdots \& 1 \\ \\vdots \& \\vdots \& \\ddots\& \\vdots \\ 1 \& 1 \& \\cdots \& 0\\end{array}\\right\]\) 记\(P=\\left\[\\begin{array}{c}0 \& 1 \&\\cdots \&1 \\1 \& 0 \& \\cdots \& 1 \\ \\vdots \& \\vdots \& \\ddots\& \\vdots \\ 1 \& 1 \& \\cdots \& 0\\end{array}\\right\]\) 即\((\\beta\_1, \\beta\_2, …, \\beta\_n) = (\\alpha\_1, \\alpha\_2, … \\alpha\_n)P\) 由于\(|P| \\neq 0\),则系数矩阵P可逆。 则\((\\beta\_1, \\beta\_2, …, \\beta\_n) P^{-1}= (\\alpha\_1, \\alpha\_2, … \\alpha\_n)\) 即向量组\(\\alpha\_1, \\alpha\_2, … \\alpha\_n\)可由向量组\(\\beta\_1, \\beta\_2, …, \\beta\_n\)表示。
则两个向量组可以互相表示,即两个向量组等价。
向量组的相关性
向量组的相关性的判断(根据秩)
向量组的线性相关性\(\\Leftrightarrow\)\(Ax=0\)是否有非零解\(\\Leftrightarrow\) \(R(A)\<n\)是否成立
可以用行列式判断秩,也可以用矩阵初等变换来看秩
例1


行列式判断秩比较简单
例2
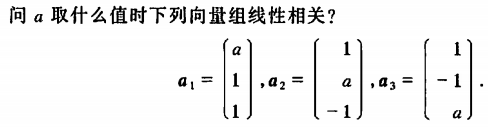
行列式=0比较简单
例3
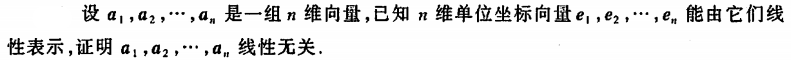
解: \(e\_{1}, e\_{2}, \\cdots, e\_{n}\)能由\(a\_{1}, a\_{2}, \\cdots, a\_{n}\)线性表示,则\(n=r(e\_{1}, e\_{2}, \\cdots, e\_{n}) \\le r(a\_{1}, a\_{2}, \\cdots, a\_{n})\) 又\(a\_{1}, a\_{2}, \\cdots, a\_{n}\)都是n维向量,则可以确定\(r(a\_{1}, a\_{2}, \\cdots, a\_{n})=n\), 则\(a\_{1}, a\_{2}, \\cdots, a\_{n}\)线性无关。
例4

向量组B线性无关 <=> (b1,b2,…,br)X=0 只有零解 <=> (a1,a2,…,as)KX = 0 只有零解 –因为 向量组A线性无关 –所以 <=> KX = 0 只有零解 <=> r(K) = r (K的列数). https://zhidao.baidu.com/question/327222311.html?seed=0
例5
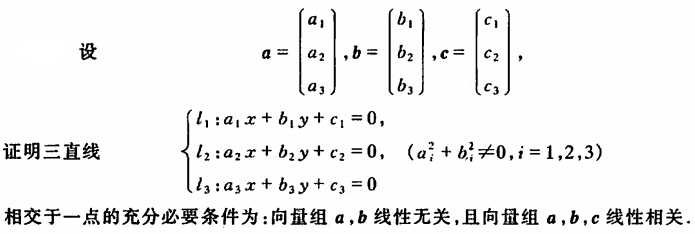

向量组的相关性的判断(反证法)
例1


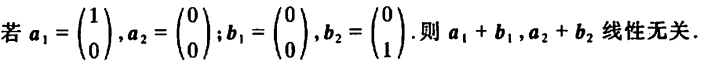
注意:0向量和任意向量都线性相关。
例2

略
例3 涉及到后面线性方程组解的结构

(1) 设非齐次线性方程组AX=b的特解为 X(0);导出组的一个基础解系为 X(1),X(2),……,X(n-r); 反设上述向量线性相关,则存在不全为零的数C(i)使得 C(0)X(0)+C(1)X(1)+C(2)X(2)+……+C(n-r)X(n-r)=0 等号两边同时乘以A,左边成为b,右边却是0。这与b不等于零向量矛盾。
(2)由(1)已知\(\\eta^{*}, \\xi\_{1}, \\cdots, \\xi\_{n-r}\)线性无关,则\(r(\\eta^{*}, \\xi\_{1}, \\cdots, \\xi\_{n-r})=n-r\), 则对应矩阵的秩也为n-r (矩阵的列向量组的秩等于矩阵的秩), 矩阵\((\\eta^{*}, \\eta^{*}+\\xi\_{1}, \\cdots, \\eta^{*}+\\xi\_{n-r})\)初等列变换可变为\((\\eta^{*}, \\xi\_{1}, \\cdots, \\xi\_{n-r})\),初等变换不改变矩阵的秩。 则矩阵的秩有\(r(\\eta^{*}, \\eta^{*}+\\xi\_{1}, \\cdots, \\eta^{*}+\\xi\_{n-r})=r(\\eta^{*}, \\xi\_{1}, \\cdots, \\xi\_{n-r})=n-r\) 则对应向量组的秩也为\(r(\\eta^{*}, \\eta^{*}+\\xi\_{1}, \\cdots, \\eta^{*}+\\xi\_{n-r})=n-r\) 则\(\\eta^{*}, \\eta^{*}+\\xi\_{1}, \\cdots, \\eta^{*}+\\xi\_{n-r}\)线性无关。
向量组的相关性的判断(代换法)
例1
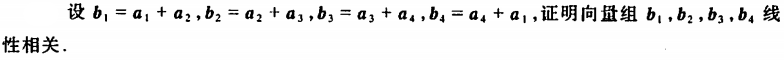
解: \(b\_4 = a\_4 + a\_1 = b\_3 – a\_3 + b\_1 – a\_2 = b\_3 + b\_1 – (a\_3 + a\_2) = b\_3 + b\_1 – b\_2\) 即\(b\_1 – b\_2+b\_3 – b\_4 = 0\) 则存在一组不全为零的系数(1,-1,1,-1)使得\(b\_{1}, b\_{2}, b\_{3}, b\_{4}\)的线性组合为0. 即\(b\_{1}, b\_{2}, b\_{3}, b\_{4}\)线性相关。
例2

b1=a1,b2=a1+a2,…..,br=a1+a2a+….+ar 设常数k1,baik2……dukr满足k1b1+k2b2+……+krbr=0 把b1,b2,……br带入中 (k1+k2+……+kr)a1+(k2+k3+……+kr)a2+……+krar=0 向量组zhia1,a2…ar线性无关 则k1+k2+……+kr=0 k2+k3+……+kr=0 …… kr=0 解得k1=0,k2=0,……kn=0 即只有全为0的常数k才能使k1b1+k2b2+……+krbr=0 向量组b1,b2,…br线性无关
向量组的秩与极大线性无关组
计算向量组的秩与极大线性无关组以及用极大线性无关组表示其他向量
向量组的秩=对应矩阵的秩;对于列向量组,初等行变换不改变各列向量之间的比例关系。
可根据矩阵的初等变换来看向量组的秩; 但是确定极大线性无关组之后,用极大无关组表示其他向量,为保持各列向量之间的比例关系,矩阵变换只能用行变换。
注意:最大无关组不唯一。
例1


例2



注意:最大无关组不唯一。
已知秩计算向量组中的参数
例1
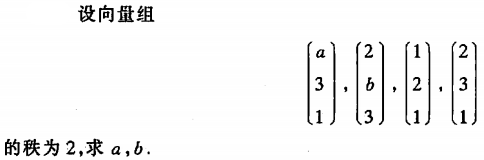

解: 向量组对应的矩阵记为A, 对A进行初等行变换。 变换过程中需要讨论a是否为0, 当a=0时,有3阶子行列式不为0,与向量组的秩=矩阵的秩=2矛盾。 则\(a\\neq 0\)。 继续初等行变换,应有两行对应成比例,或者对应位置为0, 从而得到\(a=2, b=5\)
向量组秩的证明
例1

解: \(A^2 = A\) 则\((A-E)A = 0\), 根据矩阵秩的性质八知,若 \((A-E)A = 0\) 则 \(R(\\boldsymbol{A -E})+R(\\boldsymbol{A}) \\leqslant n\) 根据矩阵秩的性质六知,\(n=R(-E)= R\[(A-E)+(-A)\] \\leqslant R(A-E) + R(A)\) 综上可知\(R(A-E) + R(A) = n\)
注: 矩阵秩的性质六:\(R(\\boldsymbol{A}+\\boldsymbol{B}) \\leqslant R(\\boldsymbol{A})+R(\\boldsymbol{B})\) 矩阵秩的性质八:若 \(\\boldsymbol{A}_{m \\times n} \\boldsymbol{B}_{n \\times l}=\\boldsymbol{O},\) 则 \(R(\\boldsymbol{A})+R(\\boldsymbol{B}) \\leqslant n\)
例2
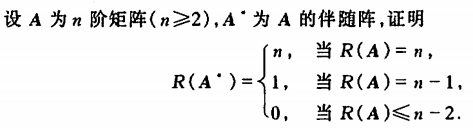
证明:(用到了矩阵秩的性质八:\(r(A)+r(A^\*)\\le n\),学完矩阵的秩和向量组之后再看这里的证明) 设A为n阶
若r(A)=n,则丨A丨不等于0,\(A^*=丨A丨A^{-1}\)可逆,推出\(r(A^*)=n\)。
若r(A)=n-2,则\(丨A丨=0\)且n-1阶子式全为0,因此\(A^*=0\),即\(r(A^*)=0\)
若r(A)=n-1,则丨A丨等于0且存在n-1阶子式不为0,因此\(A^*\)不等于0,\(r(A^*)\\ge 1\) 又因为 \(AA^*=丨A丨E=0\),\(r(A)+r(A^*)\\le n\),\(r(A^*)\\le n-r(A) = 1\) 就可以得到\(r(A^*)=1\)
线性方程组
齐次线性方程组
齐次线性方程组的通解与基础解系
例1

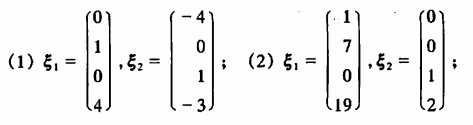

例2

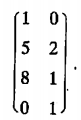
例3

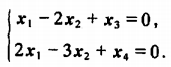
设齐次线性方程组AX=0的基础解系为a1=(0,1,2,3)T,a2=(3,2,1,0)T 即a1=(0,1,2,3)T,a2=(3,2,1,0)T是齐次线性方程组AX=0的两个特解 设A=(A1 A2)^T,其中A1,A2为4维列向量,A为2*4阶矩阵 则(A1 A2)^T * (a1 a2) = 0 等式两边同时转置得 (a1 a2)^T * (A1 A2) = 0 问题转化为求解新齐次线性方程组的基础解系 增广矩阵为 0 1 2 3 0 3 2 1 0 0 初等行变换 1 0 -1 -2 0 0 1 2 3 0 所以新齐次线性方程组的基础解系为A1=(1,-2,1,0)T,A2=(2,-3,0,1)T 所以所求的齐次线性方程组AX=0为 x1-2×2+x3=0 2×1-3×2+x4=0 原理: ξ是齐次线性方程组的解 的充要条件是 ξ与系数矩阵的行向量正交 所以只要寻找与a1,a2都正交的向量A1,A2,即可构成所求齐次线性方程组的系数矩阵 https://www.zybang.com/question/34bee07d0fbe4c454e4cf0bc4fa0f6e2.html
齐次线性方程组的公共解
参考来源:https://www.zhihu.com/question/340362949/answer/885382762
假设有A B两个矩阵,有公共解是A的解里面有部分是可以当作B的解。而同解就是A的解就是B的解。
对于求公共解的问题有三种题型。
第一种是给出了两个方程组,依次的系数矩阵为A B,则需要对A B作联立求解,类似求非齐次的求解方法,但是非齐次是列的联立,求公共解是行的联立。
第二种题型是给出了一个方程组B,和另外的一个方程组B的通解。同样的把A的通解解出来,令两个解相等,构成了新的齐次方程组,这里的未知数是就是通解上面的k,解出k1 k2的通解在代入之前的通解即可。
第三种题型,跟第二种类似了,只是给出了两个通解,方法还是类似的。令解相等,再求解,再代入。
例1

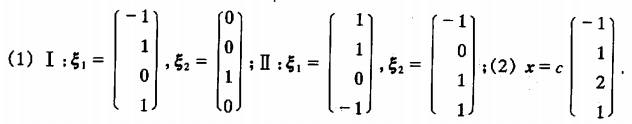
非齐次线性方程组
计算非齐次方程的通解与基础解系
例1
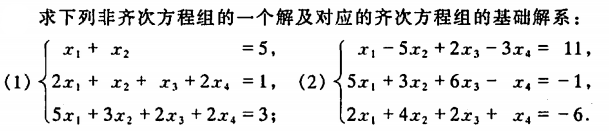

例2


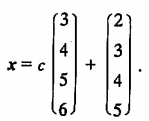
解: 设该4元非齐次线性方程组为\(Ax=b\) 则\(A(\\eta\_2+\\eta\_3) = 2b\), \(A\\eta\_1 = b\) 则\(A(\\eta\_2+\\eta\_3 – 2\\eta\_1) = 0\) 则\(kA(\\eta\_2+\\eta\_3 – 2\\eta\_1) = 0\) 则\(k(\\eta\_2+\\eta\_3 – 2\\eta\_1)\)是对应的齐次线性方程\(Ax=0\)的解。 \(k(\\eta\_2+\\eta\_3 – 2\\eta\_1)= k\\left(\\begin{array}{c}-3-4-5-6\\end{array}\\right)\) 又对应的齐次线性方程\(Ax=0\)的秩\(R\_s = n – r(A) = 4-3 = 1\) 则\(Ax=0\)的通解为:\(k\\left(\\begin{array}{c}-3-4-5-6\\end{array}\\right)=k\_1\\left(\\begin{array}{c}3\\4\\5\\6\\end{array}\\right)\) 则\(Ax=b\)的通解为:\(\\left(\\begin{array}{c}2\\3\\4\\5\\end{array}\\right)+k\_1\\left(\\begin{array}{c}3\\4\\5\\6\\end{array}\\right)\)
例3


\(a\_{1}=2 a\_{2}-a\_{3}\), 即\((a\_1,a\_2,a\_3,a\_4) \\left(\\begin{array}{c}1-2\\1\\0\\end{array}\\right)=\\left(\\begin{array}{c}0\\0\\0\\0\\end{array}\\right)\) 则\(\\left(\\begin{array}{c}1-2\\1\\0\\end{array}\\right)\)是Ax=0的一个解, 则\(k\\left(\\begin{array}{c}1-2\\1\\0\\end{array}\\right)\)是Ax=0的解, 因为\(a\_{1}=2 a\_{2}-a\_{3}\),即\(a\_1\)能用\(a\_{2}, a\_{3}, a\_{4}\)线性表示, 而\(a\_{2}, a\_{3}, a\_{4}\)线性无关, 则\(a\_{2}, a\_{3}, a\_{4}\)是A列向量组的极大线性无关组,\(r(A) = 3\) 根据齐次线性方程解的性质,齐次线性方程组解向量组的秩\(R\_s = 4-r(A) = 1\) 则\(k\\left(\\begin{array}{c}1-2\\1\\0\\end{array}\\right)\)是Ax=0的通解。
\(b=a\_1+a\_2+a\_3+a\_4\), 即\((a\_1,a\_2,a\_3,a\_4) \\left(\\begin{array}{c}1\\1\\1\\1\\end{array}\\right)=b\) 即\(\\left(\\begin{array}{c}1\\1\\1\\1\\end{array}\\right)\)是\(Ax=b\)的一个特解。 则非齐次线性方程组\(Ax=b\)的通解为:\(k\\left(\\begin{array}{c}1-2\\1\\0\\end{array}\\right)+\\left(\\begin{array}{c}1\\1\\1\\1\\end{array}\\right)\)
根据参数讨论非齐次线性方程的解
例1


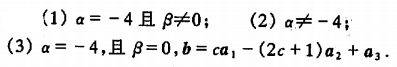
证明非齐次线性方程组的解
例1
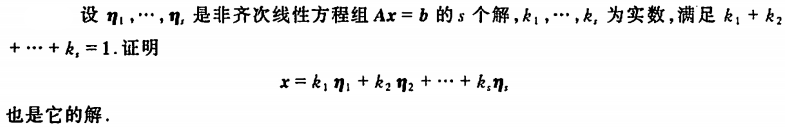
证: 已知\(x=k\_{1} \\eta\_{1}+k\_{2} \\eta\_{2}+\\cdots+k\_{s} \\eta\_{s}\) 则 \(Ax = A(k\_{1} \\eta\_{1}+k\_{2} \\eta\_{2}+\\cdots+k\_{s} \\eta\_{s}) \=A(\\eta\_{1}, \\cdots, \\eta\_s)\\left(\\begin{array}{c}k\_1\\ \\vdots\\k\_s\\end{array}\\right) \=(A\\eta\_{1}, \\cdots,A \\eta\_s)\\left(\\begin{array}{c}k\_1\\ \\vdots\\k\_s\\end{array}\\right) \=(b, \\cdots, b)\\left(\\begin{array}{c}k\_1\\ \\vdots\\k\_s\\end{array}\\right) \=k\_1 b + … + k\_s b \=(k\_1+…+k\_s)b \=b\) 即\(x=k\_{1} \\eta\_{1}+k\_{2} \\eta\_{2}+\\cdots+k\_{s} \\eta\_{s}\)是\(Ax=b\)的解。
例2

注:这里说的[题31在这里](#例3 涉及到后面线性方程组解的结构)
证明: 对于非齐次方程组(这里未知数是\(k\_1,\\cdots,k\_{n-r+1}\)): \(\\boldsymbol{x}=k\_{1} \\boldsymbol{\\eta}_{1}+\\cdots+k_{n-r+1} \\boldsymbol{\\eta}_{n-r+1}\) 即\(x=(\\eta\_1, \\cdots, \\eta_{n-r+1})\\left(\\begin{array}{c}k\_1\\ \\vdots\\k\_{n-r+1}\\end{array}\\right)\) 因为\(\\eta\_1, \\cdots, \\eta\_{n-r+1}\)线性无关,则\(r(\\eta\_1, \\cdots, \\eta\_{n-r+1})=n-r+1\) = 未知数个数 则该非齐次方程组有唯一解。 则对任意的(n-r+1)维向量x都可以用\(\\eta\_1, \\cdots, \\eta\_{n-r+1}\)线性表示,且表示法唯一。
取满足\(Ax=b\)的向量x, 则\(b=Ax=A(\\eta\_1, \\cdots, \\eta\_{n-r+1})\\left(\\begin{array}{c}k\_1\\ \\vdots\\k\_{n-r+1}\\end{array}\\right) \=(b, \\cdots, b)\\left(\\begin{array}{c}k\_1\\ \\vdots\\k\_{n-r+1}\\end{array}\\right) \=k\_1 b + \\cdots + k\_{n-r+1} b\) 则\(k\_{1}+\\cdots+k\_{n-r+1}=1\)
综上,有\(Ax=b\)的任一解都可表示为\(\\boldsymbol{x}=k\_{1} \\boldsymbol{\\eta}_{1}+\\cdots+k_{n-r+1} \\boldsymbol{\\eta}_{n-r+1}\),且\(k_{1}+\\cdots+k\_{n-r+1}=1\)
证明二: 网上找来的答案:(个人感觉答案中某些位置的\(Ax=b\)应该替换为\(Ax=0\)才对) 

向量空间
判断是否是向量空间
例1
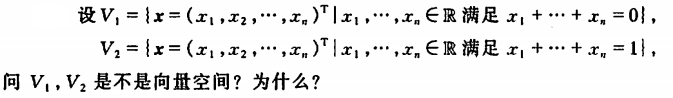

例2
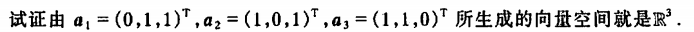

例3

证明一: 对增广矩阵\((a\_1,a\_2|b\_1,b\_2)\)初等行变换,可得\(r(a\_1,a\_2) = r(b\_1,b\_2)=r(a\_1,a\_2,b\_1,b\_2)=2\) 则向量组\(a\_1,a\_2\)与向量组\(b\_1,b\_2\)等价 根据向量空间的性质,向量组等价,生成对应的向量空间相等,即\(L\_1 = L\_2\)
证明二: 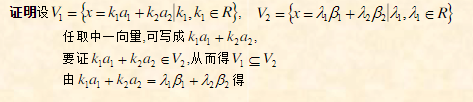

例4
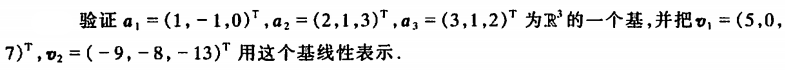

例5



发表回复