Contents

1 线性代数总结

线性代数总结

根据同济线性代数第一版的序言，线性代数本是高等数学第13章，后来提出来单独成书。

线性代数分为6块内容：行列式、矩阵、向量与向量空间、方程组、特征值、二次型。概念互相渗透，联系紧密。

行列式、矩阵、向量、方程组联系尤为紧密。向量是研究方程组的解的过程中，提炼抽象出来的。（并提出了向量的相关无关、向量的秩、矩阵的秩的概念）行列式和矩阵式求解方程组的过程中，提炼的工具。（消元的过程中，无法避免$ad-bc$的形式，将其定义为二阶行列式；系数与未知数的相乘并相加，系数提出来更简洁，就成了系数矩阵）矩阵按列分块，就变成了向量。（解方程组的问题就变成了各列向量能否线性表示b的问题）

二次型的几何意义：空间解析几何的二次曲面。

线性代数的难点和重点：

两难一重
重点一	方程组	有无解？有几个解？如何求解以及参数处理
重点二	特征值、特征向量	$A\\alpha = \\lambda \\alpha$，矩阵相似，对角阵相似。综合性强
难点	向量	线性表示、相关无关、秩

线性代数的特点： 1）概念多，定理多，运算法则多，符号多（易混淆） 2）内容上纵横交错，知识前后联系紧密（需要编织知识网络，重视一题多解）（解法灵活多变） 3）逻辑推理要求高（尤其是证明）

向量

概念,运算

线性表示

问$\\alpha\_1, \\alpha\_2 … \\alpha\_n$ 能否线性表示$\\beta$,等于问一个非齐次方程组$(\\alpha\_1, \\alpha\_2 … \\alpha\_n)X=\\beta$ 有解没解的问题.

线性相关与无关

线性相关与无关定义

设$\\alpha\_1, \\alpha\_2, … ,\\alpha\_n$ 为一组n维向量，如果存在一组不全为0的数$k\_1, k\_2, … , k\_s$，使得$k\_1 \\alpha\_1 + k\_2 \\alpha\_2 + … + k\_s \\alpha\_s = 0$ 成立，称向量组$\\alpha\_1, \\alpha\_2, … , \\alpha\_s$ 线性相关；如果上述等式仅当$k\_1 = k\_2 = … = k\_s = 0$ 时成立，则称向量组$\\alpha\_1, \\alpha\_2, … , \\alpha\_s$ 线性无关

注意这里（n和s的区别）

问$\\alpha\_1, \\alpha\_2 … \\alpha\_n$ 是否线性相关,等于问一个齐次方程组$(\\alpha\_1, \\alpha\_2 … \\alpha\_n)X=0$ 有解没解(是否只有0解)的问题.

n维向量的向量组 $\\alpha\_{1}, \\alpha\_{2} \\cdots \\alpha\_{m}$ 线性相关 $\\Leftrightarrow$ $\\exists$ 不全为0的 $k\_{1} k\_{2} \\cdots k\_{m}$ , s.t. $k\_1 \\alpha\_1 + k\_2 \\alpha\_2 + \\cdots + k\_m \\alpha\_m = 0$ $\\Leftrightarrow$ $\\exists$ 不全为0的 $k\_{1} k\_{2} \\cdots k\_{m}$ , s.t. $\\left\[\\alpha\_{1} \\alpha\_{2} \\cdots \\alpha\_{m}\\right\]\\left\[\\begin{array}{l}{k\_{1}} {k\_{2}} {k\_{m}}\\end{array}\\right\]=0$ $\\leftrightarrow$ $\\left\[\\alpha\_{1} \\alpha\_{2} \\cdots \\alpha\_{m}\\right\]\\left\[\\begin{array}{l}{x\_{1}} {x\_{2}} {x\_{m}}\\end{array}\\right\]=0$ 存在非0解 $\\Leftrightarrow$ $r\\left(\\alpha\_{1} \\alpha\_{2} \\cdots \\alpha\_{m}\\right)\<m$

推论

n个n维向量$\\alpha\_1, \\alpha\_2 … \\alpha\_n$ 相关 $\\Leftrightarrow$ $|\\alpha\_1, \\alpha\_2 … \\alpha\_n|=0$
n+1个n维向量必线性相关
$\\alpha\_1, \\alpha\_2 … \\alpha\_s$ 相关,则$\\alpha\_1, \\alpha\_2 … \\alpha\_s … \\alpha\_{s+r}$ 必相关

i.e. 方程组有非0解,添加几个未知数之后仍有非0解
低维向量线性无关,那么添加维度(坐标)后的高维向量也无关

e.g.

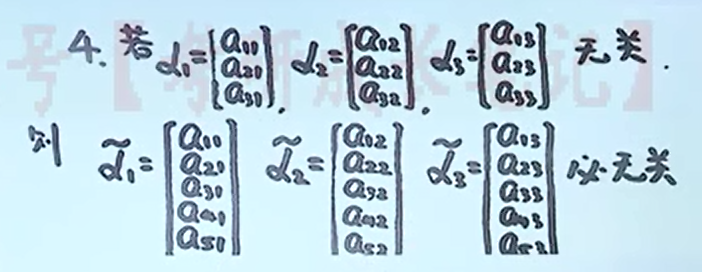
低维向量线性相关的几何意义

两个三维向量线性相关,表示向量共线(坐标成比例);

三个三维向量线性相关,表示共面(坐标成比例)

秩

极大线性无关组

设$\\alpha\_1, \\alpha\_2, .. \\alpha\_s$ 是一个n维向量组，如果向量组中有r个向量线性无关，且向量的任意$r+1$个向量线性相关，则这r个线性无关的向量称为向量组$\\alpha\_1, \\alpha\_2, .. \\alpha\_s$ 的极大线性无关组

向量组的秩

向量组$\\alpha\_1, \\alpha\_2, .. \\alpha\_s$的极大线性无关组中所含有向量的个数称为此向量组的秩，记作$r(\\alpha\_1, \\alpha\_2, .. \\alpha\_s)$ 如果一个向量组仅含有零向量，则规定它的秩为0

[等价的向量组](# 等价矩阵)具有相同的秩

矩阵的秩

矩阵列向量组的秩，或者矩阵行向量组的秩，称为矩阵的秩

矩阵的秩也可以认为是不为0的余子式的最大阶数

矩阵与向量的秩的关联

$r(A)=A的列秩=A的行秩$

矩阵等价,秩相等.

向量组等价,秩相等;秩相等,向量组不一定等价.

矩阵秩公式

$r(A^T)=r(A)$

$r(A+B)\\le r(A)+r(B)$

$r(kA)=r(A)$

$r(AB)\\le min(r(A),r(B))$

若A可逆,则 $r(AB)=r(B), r(BA)=r(B)$

$r(AA^T)=r(A)$

设A-mxn, B-nxs, 且$AB=0$, 则$r(A)+r(B) \\le n$

$\\left\[\\begin{matrix} A \& O O \& B\\end{matrix}\\right\]=r(A)+r(B)$

定理:经过初等变换,矩阵的秩不变.

向量空间

运算封闭

若从某个非空数集中任选两个元素（同一元素可重复选出），选出的这两个元素通过某种（或几种）运算后的得数仍是该数集中的元素，那么，就说该集合对于这种（或几种）运算是封闭的

向量空间

设S是n维向量的非空集合,且S中向量对于加法和数乘运算是封闭的,则称S构成一向量空间

子空间

基底

若$\\alpha\_1, \\alpha\_2, … \\alpha\_n$ 为向量空间S中的一个线性无关的向量组, 且S中任一向量可由$\\alpha\_1, \\alpha\_2, … \\alpha\_n$ 线性表示, 称$\\alpha\_1, \\alpha\_2, … \\alpha\_n$ 为向量空间中的一个基底

向量空间的维数

向量空间中,基底所含向量的个数,称为此向量空间的维数. 若$\\alpha\_1, \\alpha\_2, … \\alpha\_n$ 为向量空间S的一个基底,则其维数为n, 称为n维向量空间, 记为$R^n$

坐标

基变换与坐标变换

内积

设向量:

$\\alpha = \\left( \\begin{array} { c } { a \_ { 1 } } { a \_ { 2 } } { \\vdots } { a \_ { n } } \\end{array} \\right) , \\boldsymbol { \\beta } = \\left( \\begin{array} { c } { b \_ { 1 } } { b \_ { 2 } } { \\vdots } { b \_ { n } } \\end{array} \\right)$

则$\\alpha$ 与$\\beta$ 内积为:

$( \\boldsymbol { \\alpha } , \\boldsymbol { \\beta } ) = \\boldsymbol { \\alpha } ^ { \\mathrm { T } } \\boldsymbol { \\beta } = \\left( a \_ { 1 } , a \_ { 2 } , \\cdots , a \_ { n } \\right) \\left\[\\begin{array}{}{ b \_ { 1 } } { \\vdots } { b \_ { n } } \\end{array}\\right\] = a \_ { 1 } b \_ { 1 } + a \_ { 2 } b \_ { 2 } + \\cdots + a \_ { n } b \_ { n }$

向量的长度: $| \\boldsymbol { \\alpha } | = \\sqrt { a \_ { 1 } ^ { 2 } + a \_ { 2 } ^ { 2 } + \\cdots + a \_ { n } ^ { 2 } }$

内积性质:

$\\begin{array} { l } { ( \\boldsymbol { \\alpha } , \\boldsymbol { \\beta } ) = ( \\boldsymbol { \\beta } , \\boldsymbol { \\alpha } ) } { \\boldsymbol { \\alpha } = \\boldsymbol { 0 } \\Leftrightarrow ( \\boldsymbol { \\alpha } , \\boldsymbol { \\alpha } ) = 0 } { ( \\boldsymbol { \\alpha } , \\boldsymbol { \\beta } + \\boldsymbol { \\gamma } ) = ( \\boldsymbol { \\alpha } , \\boldsymbol { \\beta } ) + ( \\boldsymbol { \\alpha } , \\boldsymbol { \\gamma } ) } \\end{array}$

正交

若两向量内积为0,则这两个向量正交 i.e. $( \\boldsymbol { \\alpha } , \\boldsymbol { \\beta } ) = a \_ { 1 } b \_ { 1 } + a \_ { 2 } b \_ { 2 } + \\cdots + a \_ { n } b \_ { n } = 0$, 则 $\\alpha$ 与 $\\beta$正交

施密特正交化方法

设$\\alpha\_1, \\alpha\_2, …, \\alpha\_s$ 为$R^s$ 中一组线性无关的向量

令:

$\\begin{array} { l } { \\beta \_ { 1 } = \\alpha \_ { 1 } } { \\beta \_ { 2 } = \\alpha \_ { 2 } – \\frac { \\left( \\alpha \_ { 2 } , \\beta \_ { 1 } \\right) } { \\left( \\beta \_ { 1 } , \\beta \_ { 1 } \\right) } \\beta \_ { 1 } } { \\cdots } { \\beta \_ { s } = \\alpha \_ { s } – \\frac { \\left( \\alpha \_ { s } , \\beta \_ { 1 } \\right) } { \\left( \\beta \_ { 1 } , \\beta \_ { 1 } \\right) } \\beta \_ { 1 }\\cdots – \\frac { \\left( \\alpha \_ { s } , \\beta \_ { s – 1 } \\right) } { \\left( \\beta \_ { s – 1 } , \\beta \_ { s – 1 } \\right) } \\beta \_ { s – 1 } } \\end{array}$

则 $\\beta\_1, \\beta\_2, … \\beta\_s$ 相互正交

规范正交基

设 $\\alpha\_1, \\alpha\_2, …, \\alpha\_n$ 为$R^n$ 中一组基(底)

将其(施密特)正交化得 $\\beta\_1, \\beta\_2, …, \\beta\_n$

再将其单位化得$\\boldsymbol { \\eta } \_ { 1 } = \\frac { \\boldsymbol { \\beta } \_ { 1 } } { \\left| \\boldsymbol { \\beta } \_ { 1 } \\right| }, \\eta \_ { 2 } = \\frac { \\beta \_ { 2 } } { \\left| \\beta \_ { 2 } \\right| } , \\cdots , \\eta \_ { n } = \\frac { \\beta \_ { n } } { \\left| \\beta \_ { n } \\right| }$

则$\\eta\_1, \\eta\_2, … , \\eta\_n$ 满足 $(\\eta\_i, \\eta\_j)=0, i \\neq j ; |\\eta\_i|=1, i=1,2, … , n$

称$\\eta\_1, \\eta\_2, … , \\eta\_n$ 为 $R^n$ 中的一组规范正交基

正交矩阵

定义设 $\\eta\_1, \\eta\_2, … , \\eta\_n$ 为 $R^n$ 中的一组规范正交基,令$Q=\[\\eta\_1, \\eta\_2, … , \\eta\_n\]$ , 则Q满足$Q^T Q = Q Q^T = E$ , 称为正交矩阵

如果n阶矩阵A满足$A^T A = E$，即($A^{-1} = A^T$),那么称A为正交矩阵，简称正交阵

方阵A为正交矩阵$\\Leftrightarrow$ A的列向量/行向量都是单位向量，且两两正交

正交矩阵性质:

$\\begin{array} { l } { Q ^ { \\mathrm { T } } = Q ^ { – 1 } \\quad (Q^T Q=E)} { | Q | = \\pm 1 } \\end{array}$

若$Q\_1, Q\_2$ 为正交矩阵, 则 $Q\_1, Q\_2$仍为正交矩阵

相关链接:相似矩阵与二次型的转换

线性方程组

线性方程组概念

线性方程组同解变形(矩阵行变换)

两个方程互换位置
非零常数乘到方程的两端
某方程的k被加到另一个方程上

齐次方程组$Ax=0$

无解,0解(唯一解),非零解

定理齐次方程组$A\_{m\\times n}x=0$ 有非零解 $\\Leftrightarrow$ $r(A)\<n$

推论当$m\<n$ 时, $Ax=0$ 必有非零解 (i.e. 方程组数小于未知数个数)

推论当m=n时, $Ax=0$ 有非零解 $\\Leftrightarrow$ $|A|=0$

解的性质

if $\\eta$ is solution of $Ax=0$ , then $k\\eta$ is solution, too.

if $\\eta\_1, \\eta\_2$ is solution of $Ax=0$, then $k\_1\\eta\_1 + k\_2\\eta\_2$ is solution, too.

基础解系

齐次方程组的基础解系:方程组解向量的极大线性无关组

i.e.

$\\eta\_1, \\eta\_2, … \\eta\_t$ 是 $Ax=0$ 的解
$\\eta\_1, \\eta\_2, … \\eta\_t$ 线性无关
$Ax=0$ 的任意一个解都可以由 $\\eta\_1, \\eta\_2, … \\eta\_t$ 线性表出

齐次方程组解向量的极大线性无关组(基础解系)个数$n-r(A)$

定理如果齐次方程组 $Ax=b \\quad(II)$ 系数矩阵的秩 $r(A)=r\<n$ , 则$II$ 有 $n-r$ 个线性无关的解,且 $II$ 的任意一个解都可以由这$n-r$ 个线性无关的解(基础解系)线性表出

定理若 $\\eta\_1, \\eta\_2, \\cdot\\cdot\\cdot \\eta\_t$ 是齐次方程组 $II$ 的基础解系,则 $II$ 的通解是是: $k\_1 \\eta\_1 + k\_2 \\eta\_2 + \\cdot \\cdot \\cdot + k\_t \\eta\_t$, $k\_1, k\_2, … , k\_t$ 是任意常数

非齐次方程组$Ax=b$

有解判定: 无解,唯一解, 无穷多解

定理 $A x=b$ 有解 $\\Leftrightarrow r(A)=r(\\overline A)$

唯一解: $r(A)=r(\\bar{A})=n$

$\\infty$ 解: $r(A)=r(\\bar{A})\<n$

无解: $r(A)+1=r(\\bar{A})$

解的形式

解的性质

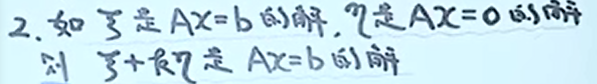
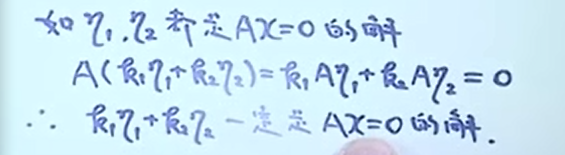
解的结构

定理设$\\alpha$ 是方程组$Ax=b$ 的解, $\\eta\_{1}, \\eta\_{2}, \\cdots, \\eta\_{t}$ 是导出组$Ax=0$ 的基础解系,则方程组$Ax=b$ 的通解为 $\\alpha+k\_{1} \\eta\_{1}+k\_{2} \\eta\_{2} \\cdots+k\_{t} \\eta\_{t}$ , 其中 $k\_{1} k\_{2} \\cdots k\_{t}$ 是任意常数

求解非齐次方程组做两件事:非齐次方程组求一个特解,求齐次方程组的基础解系,并用k衔接

公共解,同解

应用

相关无关$\\Leftrightarrow$ 齐次方程组 $(\\alpha\_1, \\alpha\_2, \\cdot\\cdot\\cdot \\alpha\_s)x=0$有非零解
线性无关$\\Leftrightarrow$ 非齐次方程组 $(\\alpha\_1, \\alpha\_2, \\cdot\\cdot\\cdot \\alpha\_s)x=\\beta$ 有没有解
$AP=B\\neq P$
$A \\alpha = \\lambda x$ 求x

特征值与特征向量

定义

$A \\alpha=\\lambda \\alpha, \\alpha \\neq 0$, 注意特征向量不为0

说明（标准定义）：设A是n阶矩阵, $\\alpha$是n维非0列向量,满足: $A \\alpha=\\lambda \\alpha$, 则称$\\lambda$是矩阵A的特征值, $\\alpha$是矩阵A属于特征值$\\lambda$的特征向量

性质

$A \\alpha=\\lambda \\alpha, \\alpha \\neq 0 \\Rightarrow (A+k E) \\alpha=(\\lambda+k) \\alpha$

$A \\alpha=\\lambda \\alpha, \\alpha \\neq 0 \\Rightarrow A^{n} \\alpha=\\lambda^{n} \\alpha$

$|A|=\\prod \\lambda$[^3](<矩阵特征值乘积等于矩阵行列式乘积的证明>)

$A \\alpha=\\lambda \\alpha, \\alpha \\neq 0 \\Rightarrow A^{-1} \\alpha=\\frac{1}{\\lambda} \\alpha$

若A可逆, $\\lambda$ 是A的特征值, 则 $\\frac{|A|}{\\lambda}$ 是$A^\*$ 的特征值

性质总结：

设$\\lambda$是矩阵A的特征值，则矩阵$kA, A^2, aA+bE, A^m, A^{-1}, A\*$ ，分别有特征值 $k\\lambda, \\lambda^2, a\\lambda+b, \\lambda^m, \\frac{1}{\\lambda}, \\frac{|A|}{\\lambda}$

设$\\alpha$是A对应$\\lambda$的特征向量，则$\\alpha$也是矩阵$kA, A^2, aA+bE, A^m, A^{-1}, A\*$对应特征值$k\\lambda, \\lambda^2, a\\lambda+b, \\lambda^m, \\frac{1}{\\lambda}, \\frac{|A|}{\\lambda}$的特征向量

不同特征值的特征向量必正交

特征值之和等于矩阵的迹

求特征值与特征向量

利用定义与性质

利用定义式的变形得行列式求特征值（解行列式=0）

$\\begin{array}{l}{ {\\left(\\lambda\_{i} E-A\\right) x=0} \\quad (x \\neq 0)\\ \\Rightarrow | \\lambda E-A |=0} \\ \\end{array}$

再分别代入特征值$\\lambda\_i$，利用定义式的变形求特征向量（解齐次方程组）

${\\left(\\lambda\_{i} E-A\\right) x=0} \\quad (x \\neq 0)$

相似矩阵

定义:

$A \\sim B:$ A, B都是n阶方阵, $\\exists$ 可逆$P, P^{-1} A P=B$ , 称A相似于B

$A \\sim \\Lambda$

矩阵相似的性质:

$A \\sim A$
$A \\sim B \\Rightarrow B \\sim A$
$A \\sim B, B \\sim C \\Rightarrow A \\sim C$ (e.g. $A \\sim \\Lambda, B \\sim \\Lambda \\Rightarrow A \\sim B$ 多用来证明)
$A \\sim B \\Rightarrow A + kE \\sim B + kE$

proof: $P ^ { – 1 } ( A + k E ) P = P ^ { – 1 } A P + P ^ { – 1 } k E P = B + k E$

$A \\sim B \\Rightarrow A^n \\sim B^n$ proof: $A \sim B \Rightarrow P^{-1}AP=B \quad (两边平方) \Rightarrow (P^{-1}AP)2=B^2 $, 数学归纳得原式
$A \\sim B \\Rightarrow \\begin{equation} |\\lambda E-A|=|\\lambda E-B| \\Rightarrow \\lambda\_{A}=\\lambda\_{B} \\end{equation}$ proof: $\\begin{aligned}|\\lambda E-B| \&=\\left|\\lambda E-P^{-1} A P\\right| \\ \&=\\left|P^{-1}(\\lambda E-A) P\\right| \\ \&=\\left|P^{-1}\\right|\\cdot|\\lambda E-A|\\cdot|P| \\ \&=|\\lambda E-A| \\end{aligned}$
$A \\sim B \\Rightarrow r(A)=r(B)$ proof: $r(B)=r\\left(P^{-1} A P\\right) \=r(A P) \=r(A)$
$A \\sim B \\Rightarrow |A|=|B|$ proof: $|B|=|P^{-1} A P| = |P^{-1} | \\cdot |A| \\cdot |P| = |A|$
$A \\sim B \\Rightarrow \\sum a\_{i i}=\\sum b\_{i i}$ (迹的和相等)

即：A相似B，{反身，传递，倍加E，n次}仍相似，相似则{特征值，秩，行列式，迹}相等。

性质推广

$A \\sim B \\Rightarrow A^{-1} \\sim B^{-1}$

证明：
$\\begin{array}{l}{\\left(P^{-1} A P\\right)^{-1}=B^{-1}} \\ {P^{-1} A^{-1}\\left(P^{-1}\\right)^{-1}=B^{-1}} \\ {P^{-1} A^{-1} P=B^{-1}} \\ {\\therefore A^{-1} \\sim B^{-1}}\\end{array}$

$A \sim B \Rightarrow A^T \sim B^T $

证明:
令$\\left(P^{T} \\right)^{-1}=P\_1$
则$P\_1^{-1} A^T P\_1 = B^T$
$A \\sim B \\Rightarrow A^\* \\sim B^\*$
若$\\mathbf{A} \\sim \\boldsymbol{B}, \\boldsymbol{C} \\sim \\boldsymbol{D}$，则$\\left\[\\begin{array}{ll}{A} \& {0} \\ {0} \& {C}\\end{array}\\right\] \\sim\\left\[\\begin{array}{ll}{B} \& {0} \\ {0} \& {D}\\end{array}\\right\]$
若$\\mathbf{A} \\sim B$，则$f(\\boldsymbol{A}) \\sim f(\\boldsymbol{B}),|f(\\boldsymbol{A})|=|f(\\boldsymbol{B})|$，其中$f(\\boldsymbol{A})$为矩阵

相似对角化

相似对角化$P^{-1} A P = \\Lambda$的方法

设$\\alpha \_ { 1 } , \\alpha \_ { 2 } , \\cdots , \\alpha \_ { n }$为对应于特征值$\\lambda\_i(i=1,2,…,n)$的特征向量 $\\begin{aligned} A \\left( \\alpha \_ { 1 } , \\alpha \_ { 2 } , \\cdots , \\alpha \_ { n } \\right) \& = \\left( A \\alpha \_ { 1 } , A \\alpha \_ { 2 } , \\cdots , A \\alpha \_ { n } \\right) \\ \& = \\left( \\lambda \_ { 1 } \\alpha \_ { 1 } , \\lambda \_ { 2 } \\alpha \_ { 2 } , \\cdots , \\lambda \_ { n } \\alpha \_ { n } \\right) \& =\\left\[ \\boldsymbol { a } \_ { 1 } , \\boldsymbol { \\alpha } \_ { 2 } , \\cdots , \\boldsymbol { \\alpha } \_ { n } \\right\] \\left\[ \\begin{array} { c c c c } { \\lambda \_ { 1 } } \\ { } \& { \\lambda \_ { 2 } } \\ { } \& { } \& { \\ddots } \\ { } \& { } \& { } \& { \\lambda \_ { n } } \\end{array} \\right\] \\end{aligned}$ 记$P = \\left\[ \\alpha \_ { 1 } , \\alpha \_ { 2 } , \\cdots , \\alpha \_ { n } \\right\]$, 记$\\boldsymbol { \\Lambda } = \\left\[ \\begin{array} { c c c c } { \\lambda \_ { 1 } } \\ { } \& { \\lambda \_ { 2 } } \\ { } \& { } \& { \\ddots } \\ { } \& { } \& { } \& { \\lambda \_ { n } } \\end{array} \\right\]$，

则$P^{-1} A P = \\Lambda$

性质

$A \sim \Lambda \Leftrightarrow $ A有n个线性无关的特征向量

$\\lambda$是k重特征值，则 $\\lambda$有k个无关的特征向量 $\\Leftrightarrow A \\sim \\Lambda$

A有n个不同的特征值$ \Rightarrow A \sim \Lambda$

A为对称矩阵 $\\Rightarrow A \\sim \\Lambda$

若$P^{-1} A P = \\Lambda$，则$\\Lambda$的主对角线上元素就是A的特征值，P的列向量就是A的特征向量[^2](<这也是构造可逆矩阵P和对角矩阵$\\Lambda$的方法>)

相似对角化可以用来求方阵的n次

实对称矩阵

如果有n阶矩阵A，其矩阵的元素都为实数，且矩阵A的转置等于其本身（$a\_{ij}=a\_{ji}$）(i,j为元素的脚标），则称A为实对称矩阵（即$A^T=A$且元素为实数的矩阵）

特点

特征值必是实数

不同特征值的特征向量必正交

必与对角矩阵相似

可用正交矩阵相似对角化[^1](（一般的相似对角化是用特征向量可逆矩阵来实现相似对角化）)

实对称矩阵用正交矩阵对角化的方法

求A的特征值$\\lambda\_1, \\lambda\_2, … \\lambda\_n$
求特征向量$\\alpha\_1, \\alpha\_2 , … \\alpha\_n$
改造特征向量为$\\gamma\_1, \\gamma\_2, … , \\gamma\_n$
1. 如$\\lambda\_i \\neq \\lambda\_j$，只需单位化
2. 如$\\lambda\_i = \\lambda\_j$
  1. 若$(\\alpha\_i, \\alpha\_j) = 0$，只需单位化
  2. 若$\\alpha\_i, \\alpha\_j) \\neq 0$，施密特正交化，单位化
构造正交矩阵$Q=(\\gamma\_1, \\gamma\_2, … , \\gamma\_n)$
得$Q^{-1} A Q = \\Lambda = \\left\[ \\begin{array} { c c c c } { \\lambda \_ { 1 } } \& { 0 } \& { \\cdots } \& { 0 } \\ { 0 } \& { \\lambda \_ { 2 } } \& { \\cdots } \& { 0 } \\ { \\vdots } \& { \\vdots } \& { \\vdots } \& { \\vdots } \\ { 0 } \& { 0 } \& { \\cdots } \& { \\lambda \_ { n } } \\end{array} \\right\]$

二次型

概念、定理

二次型及其矩阵表示

设一个多元函数，其每一项都是二次的，这样的多元函数，称作二次型；任何一个二次型都可以用矩阵的乘法描写出来。

二次型矩阵化

n元二次型

$f(x\_1, x\_2,…,x\_n) = \\Sigma{C\_{ii} x\_i x\_i} + \\Sigma{C\_{ij} x\_i x\_j} \= \[x\_1, x\_2, … , x\_n\] A \[x\_1, x\_2, … , x\_n\]^T \= x^T A x$ 其中A为一个对称矩阵，有 $A(i,i) = C\_{ii}, A(i,j) = A(j,i) = C\_{ij}/2$

函数f的平方项$C\_{ii} x\_i x\_i$系数依次填入对称矩阵P的对角线，函数f的混合项$C\_{ij} x\_i x\_j$系数除以2，分别填入矩阵A对应位置

这里的矩阵A称为二次型的矩阵

i.e. 一个三元二次型： $\\begin{aligned} f\\left(x\_{1}, x\_{2}, x\_{3}\\right)=\& x\_{1}^{2}+5 x\_{2}^{2}+5 x\_{3}^{2}+2 x\_{1} x\_{2}-6 x\_{2} x\_{3} \\ \&=\\left\[x\_{1} x\_{2} x\_{3}\\right\]\\left\[\\begin{array}{ccc}{1} \& {1} \& {0} \\ {1} \& {5} \& {-3} \\ {0} \& {-3} \& {5}\\end{array}\\right\]\\left\[\\begin{array}{c}{x\_{1}} \\ {x\_{2}} \\ {x\_{3}}\\end{array}\\right\] \\end{aligned}$

标准型

只有平方项，没有混合项的二次型

则标准型对应的矩阵是个对角矩阵

规范型

平方项系数只能为0，+1，-1的标准型

惯性指数

正惯性指数：标准型中正的二次项个数

负惯性指数：标准型中负的二次项个数

二次型的秩

$r(f)=r(A)$

坐标变换

以3元坐标为例：

$\\left{\\begin{array}{l}{x\_{1}=c\_{11} y\_{1}+c\_{12} y\_{1}+c\_{13} y\_{3}} \\ {x\_{2}=c\_{21} y\_{1}+c\_{22} y\_{2}+c\_{23} y\_{3}} \\ {x\_{3}=c\_{31} y\_{1}+c\_{32} y\_{2}+c\_{33} y\_{3}}\\end{array} \\quad|C| \\neq 0\\right.$

$\\left\[\\begin{array}{l}{x\_{1}} \\ {x\_{2}} \\ {x\_{3}}\\end{array}\\right\]=\\left\[\\begin{array}{lll}{C\_{11}} \& {C\_{12}} \& {C\_{13}} \\ {C\_{21}} \& {C\_{22}} \& {C\_{23}} \\ {C\_{31}} \& {C\_{32}} \& {C\_{33}}\\end{array}\\right\]\\left\[\\begin{array}{l}{y\_{1}} \\ {y\_{2}} \\ {y\_{3}}\\end{array}\\right\]$

那么通过坐标变换 $x=Cy$，把坐标x用矩阵C变换为了y的坐标，这里要求C可逆

对二次型做坐标变换： $\\left{ \\begin{array} { l } { f ( x ) = x ^ { T } A x } \\ { x = C y , | C | \\neq 0 } \\end{array} \\right.$ $\\Rightarrow \\begin{aligned} g ( y ) = f \\left( C \_ { y } \\right) \& = \\left( C y \\right) ^ { T } A \\left( C y \\right) \& = y ^ { T } C ^ { T } A C y \& = y ^ { T } B y \\end{aligned}$ 其中$B=C^T A C$

矩阵合同

由对二次型的[坐标变换](# 坐标变换)可知，坐标变换${ x = C y , | C | \neq 0 } $时，二次型的矩阵A也变为B，并满足$B=C^T A C$

定义

如果$C^{T} A C=B$，其中C是可逆矩阵，称矩阵A和B合同，记$A \\simeq B$

$A \simeq B \Leftrightarrow $ $x^T A x $ 与 $x^T B x$ 正负惯性指数相同

性质

$A \\simeq A$

如果$A \\simeq B$，则$B \\simeq A$

如果$A \\simeq B, B \\simeq C$，则$A \\simeq C$

任一实对称矩阵必合同于一个对角矩阵

定理 $x^T A x $ 经坐标变换$x=Cy$，有$x^T A x = y^T B y$，其中$C^T A C = B$

即二次型经坐标变换，二次型的矩阵变换为它的合同矩阵

定理对任意$x^T A x$，都存在坐标变换$x=Cy$，使得$f=y^T \\Lambda y$

即任意二次型都可以找到坐标变换，化为标准型

定理（惯性定理）对于一个二次型$x^T A x$，经坐标变换化为标准型，其正惯性指数和负惯性指数都是唯一确定的

二次型变换为标准型的方法是不唯一的，即可能化为不同的标准型。但是这些标准型的正惯性指数和负惯性指数都是唯一确定的。

二次型变换为标准型

配方法

正交变换法

求特征值$\\lambda\_1, \\lambda\_2, … , \\lambda\_n$
求特征向量$\\alpha\_1, \\alpha\_2, … , \\alpha\_n$
改造特征向量（正交化，单位化）为$\\gamma\_1, \\gamma\_2, … , \\gamma\_n$
1. 特征值不同，特征向量已正交，只需单位化
2. 特征值有重根
  1. 该特征值的多个特征向量正交，只需单位化
  2. 该特征值的多个特征向量不正交，施密特正交化，并单位化
拼称正交矩阵$Q=(\\gamma\_1, \\gamma\_2, …, \\gamma\_n)$
令$x=Qy$，得$x^T A x = y^T \\Lambda y, \\Lambda = \\left\[ \\begin{array} { c c c c } { \\lambda \_ { 1 } } \& { 0 } \& { \\cdots } \& { 0 } \\ { 0 } \& { \\lambda \_ { 2 } } \& { \\cdots } \& { 0 } \\ { \\vdots } \& { \\vdots } \& { \\vdots } \& { \\vdots } \\ { 0 } \& { 0 } \& { \\cdots } \& { \\lambda \_ { n } } \\end{array} \\right\]$

简证：正交矩阵Q有$Q^T = Q^{-1}$的性质，结合[相似对角化](# 相似对角化)的证明过程，可知以上正交变换法是正确的

正定二次型

正定二次型定义

$\\forall x = (x\_1, x\_2, … , x\_n)^T \\neq 0$，恒有$f(x\_1, x\_2, … , x\_n) = x^T A x \> 0$，则称f为正定二次型，A为正定矩阵

性质

合同变换不改变二次型的正定性

$x^T A x$正定二次型 $\\Leftrightarrow$ 正惯性指数p=n $\\Leftrightarrow$ $A \\simeq E \\quad (i.e. \\exists |C| \\neq 0, C^T A C = E)$ $\\Leftrightarrow$ A的特征值全大于0 $\\Leftrightarrow$ A的顺序主子式全大于0 $\\Leftrightarrow$ 存在可逆矩阵P，使$A = P^T P$ $\\Leftrightarrow$ 存在正交矩阵Q，使$\\boldsymbol{Q}^{\\mathrm{T}} \\boldsymbol{A Q}=\\boldsymbol{Q}^{-1} \\mathrm{AQ}=\\left\[\\begin{array}{ccc}{\\lambda\_{1}} \& {} \& {} \\ {} \& {\\lambda\_{2}} \& {} \\ {} \& {} \& {\\ddots} \& {} \\ {} \& {} \& {} \& {\\lambda\_{n}}\\end{array}\\right\], \\lambda\_{i}\>0(i=1,2, \\cdots, n)$

若A为正定矩阵，则$k \\mathbf{A}(k\>0), \\mathbf{A}^{\\mathrm{T}}, \\mathbf{A}^{-1}, \\mathbf{A}^{\*}$也是正定矩阵[^4](A正定，证明$A^{-1}$正定) 若A为正定矩阵，则$|A|\>0$，从而A可逆若A为正定矩阵，则A的主对角线上元素$a\_{i i}\>0, i=1,2, \\cdots, n$

$(A^{-1})^T = (A^T)^{-1} \\overset{A \\text{正定}}{=} A^{-1}$ 所以$A^{-1}$是对称矩阵
设$\\lambda$是$A^{-1}$的特征值， $\\alpha$是对应的特征向量 $\\therefore A^{-1} \\alpha = \\lambda \\alpha$ $\\because$ A正定，其特征孩子全大于0 $\\therefore$ A的特征值$\\frac{1}{\\lambda} \> 0$ $\\therefore \\lambda \> 0$ $\\therefore A^{-1}$正定

易混概念辨析

矩阵等价,合同,相似

矩阵等价 : 对同型矩阵A、B，存在可逆阵P和Q，使得B=PAQ 充要条件：A和B的秩相等理解: 初等变换(行/列变换), 不改变矩阵的秩,变换前后的矩阵等价

[矩阵合同](# 矩阵合同): 对同型方阵A、B，存在可逆阵P, 使得$B=P^T A P$

[矩阵相似](# 相似矩阵): 对同型方阵A、B，存在可逆阵P, 使得$B=P^{-1}AP, \\quad B=P^{-1}AP$

三者关系：

等价（只有秩相同）–>合同（秩和正负惯性指数相同）–>相似（秩，正负惯性指数，特征值均相同），矩阵亲密关系的一步步深化。

相似矩阵必为等价矩阵，但等价矩阵未必为相似矩阵 PQ=EPQ=E 的等价矩阵是相似矩阵合同矩阵必为等价矩阵，等价矩阵未必为合同矩阵正惯性指数相同的等价矩阵是合同矩阵合同矩阵未必是相似矩阵相似矩阵未必合同正交相似矩阵必为合同矩阵，正交合同矩阵必为相似矩阵如果A与B都是n阶实对称矩阵，且有相同的特征根．则A与B既相似又合同

方程组系数矩阵的秩,方程组解的秩

对于齐次方程组: \[
\\left{ \\begin{array} { l } { x \_ { 1 } – x \_ { 2 } + 2 x \_ { 3 } – 3 x \_ { 4 } = 0 } \\
{ 2 x \_ { 1 } – 2 x \_ { 2 } + 4 x \_ { 3 } + 6 x \_ { 4 } = 0 } \\end{array} \\right.
\] 其系数矩阵: \[
A=\\left\[\\begin{array}{rrrr}{1} \& {-1} \& {2} \& {-3} \\
{2} \& {-2} \& {4} \& {6}\\end{array}\\right\]\\rightarrow\\left\[\\begin{array}{rrrr}{1} \& {-1} \& {2} \& {-3} \\
{0} \& {0} \& {0} \& {12}\\end{array}\\right\]\\rightarrow\\left\[\\begin{array}{rrrr}{1} \& {-1} \& {2} \& {0} \\
{0} \& {0} \& {0} \& {1}\\end{array}\\right\]
\]

系数矩阵A的秩:$r(A)=2$

方程组系数矩阵A(或者A的列向量)的极大线性无关组: $\\left\[\\begin{array}{l}{1} {2}\\end{array}\\right\],\\left\[\\begin{array}{r}{-3} {6}\\end{array}\\right\]$

方程组极大线性无关组(基础解系)个数，即解的秩: $n-r(A)=4-2=2$ $\\begin{array}{l}{x\_{2}=1, x\_{3}=0} \\quad \\rightarrow {\\eta\_{1}=(1,1,0,0)^{T}} {x\_{2}=0, x\_{3}=1} \\quad \\rightarrow {\\eta\_{2}=(-2,0,1,0)^{T}}\\end{array}$

方程组解向量的极大线性无关组(基础解系): $\\left\[\\begin{array}{c}{1} {1} {0} {0}\\end{array}\\right\],\\left\[\\begin{array}{c}{-2} {0} {1} {0}\\end{array}\\right\]$

秩,极大线性无关组个数,系数矩阵的秩，方程组的基础解系

线性无关(组)：仅当$k\_1 = k\_2 = … = k\_s = 0$ 时, 得$k\_1 \\alpha\_1 + k\_2 \\alpha\_2 + … + k\_s \\alpha\_s = 0$ 成立，称向量组$\\alpha\_1, \\alpha\_2, … , \\alpha\_s$ 线性无关

[极大线性无关组](# 极大线性无关组)：向量组中有r个向量线性无关，且向量的任意$r+1$个向量线性相关，这r个线性无关的向量称为向量组的极大线性无关组

[秩](# 秩)：极大线性无关组中向量的个数

(方程组$Ax=\\beta$的)系数矩阵：A

(方程组$Ax=\\beta$的)增广矩阵：$(A|\\beta)$

(方程组$Ax=\\beta$的)基础解系：方程组解空间的极大线性无关组

(方程组$Ax=\\beta$的)系数矩阵的秩：$r(A)$

(方程组$Ax=\\beta$的)基础解系的秩：$n-r(A)$

行列式同等变形, 矩阵行/列变换, 方程组同解变形

说明

(行/列)倍乘: 非零元素乘以某一行(列)

(行/列)倍加: 非零元素乘以某一行(列),加到另一行(列)上

(行/列)互换: 某一行(列)与另一行(列)位置互换

区别

矩阵行/列变换

不是同等变形(变形前后不是“=”关系)

变换规则:倍乘, 倍加, 互换

有些情况只能行变换 e.g. 增广矩阵变换$(A|\\beta) \\rightarrow (E|\\beta')$, 矩阵求逆$(A|E)\\rightarrow (E|A^{-1})$

行列式同等变形

是同等变形

变形规则: (行/列)倍乘, (行/列)倍加, (行/列)互换(互换位置行列式取反)

方程组同解变形

是同等变形

变形规则: 行倍乘, 行倍加, 行互换

[极大线性无关组]:

线性代数总结

线性代数总结

向量

概念,运算

线性表示

问\(\\alpha\_1, \\alpha\_2 … \\alpha\_n\) 能否线性表示\(\\beta\),等于问一个非齐次方程组\((\\alpha\_1, \\alpha\_2 … \\alpha\_n)X=\\beta\) 有解没解的问题.

线性相关与无关

线性相关与无关定义

问\(\\alpha\_1, \\alpha\_2 … \\alpha\_n\) 是否线性相关,等于问一个齐次方程组\((\\alpha\_1, \\alpha\_2 … \\alpha\_n)X=0\) 有解没解(是否只有0解)的问题.

低维向量线性相关的几何意义

两个三维向量线性相关,表示向量共线(坐标成比例);

三个三维向量线性相关,表示共面(坐标成比例)

秩

极大线性无关组

向量组的秩

矩阵的秩

矩阵与向量的秩的关联

\(r(A)=A的列秩=A的行秩\)

矩阵秩公式

定理:经过初等变换,矩阵的秩不变.

向量空间

运算封闭

向量空间

子空间

基底

向量空间的维数

坐标

基变换与坐标变换

内积

正交

施密特正交化方法

规范正交基

正交矩阵

定义 设 \(\\eta\_1, \\eta\_2, … , \\eta\_n\) 为 \(R^n\) 中的一组规范正交基,令\(Q=\[\\eta\_1, \\eta\_2, … , \\eta\_n\]\) , 则Q满足\(Q^T Q = Q Q^T = E\) , 称为正交矩阵

正交矩阵性质:

线性方程组

线性方程组概念

线性方程组同解变形(矩阵行变换)

齐次方程组\(Ax=0\)

无解,0解(唯一解),非零解

定理 齐次方程组\(A\_{m\\times n}x=0\) 有非零解 \(\\Leftrightarrow\) \(r(A)\<n\)

解的性质

基础解系

齐次方程组的基础解系:方程组解向量的极大线性无关组

齐次方程组解向量的极大线性无关组(基础解系)个数\(n-r(A)\)

相关无关

非齐次方程组\(Ax=b\)

有解判定: 无解,唯一解, 无穷多解

解的形式

解的性质

解的结构

公共解,同解

应用

特征值与特征向量

定义

性质

求特征值与特征向量

相似矩阵

定义:

矩阵相似的性质:

性质推广

相似对角化

性质

实对称矩阵

特点

实对称矩阵用正交矩阵对角化的方法

二次型

概念、定理

二次型及其矩阵表示

二次型矩阵化

标准型

规范型

惯性指数

二次型的秩

坐标变换

矩阵合同

定义

性质

定理 $x^T A x $ 经坐标变换\(x=Cy\)， 有\(x^T A x = y^T B y\)， 其中\(C^T A C = B\)

定理 对任意\(x^T A x\)， 都存在坐标变换\(x=Cy\)，使得\(f=y^T \\Lambda y\)

定义设 \(\\eta\_1, \\eta\_2, … , \\eta\_n\) 为 \(R^n\) 中的一组规范正交基,令\(Q=\[\\eta\_1, \\eta\_2, … , \\eta\_n\]\) , 则Q满足\(Q^T Q = Q Q^T = E\) , 称为正交矩阵

定理齐次方程组\(A\_{m\\times n}x=0\) 有非零解 \(\\Leftrightarrow\) \(r(A)\<n\)

定理 $x^T A x $ 经坐标变换\(x=Cy\)，有\(x^T A x = y^T B y\)，其中\(C^T A C = B\)

定理对任意\(x^T A x\)，都存在坐标变换\(x=Cy\)，使得\(f=y^T \\Lambda y\)

定理（惯性定理）对于一个二次型\(x^T A x\)，经坐标变换化为标准型，其正惯性指数和负惯性指数都是唯一确定的

发表回复取消回复