Contents
高等数学-多元微积分-曲线积分与曲面积分习题
对弧长的曲线积分
平面上对弧长的曲线积分
定积分法计算曲线积分
例1
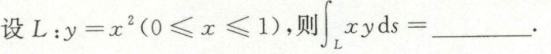

例2
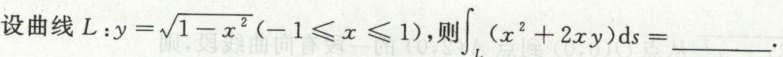
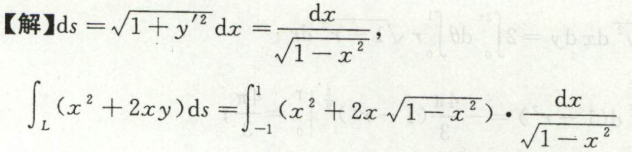
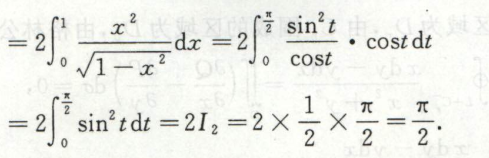
本题也可以利用奇偶对称性消去积分中的\(2xy\)项,并把曲线表示为$x=\cos t , y = \sin t $的参数方程来做。
例3

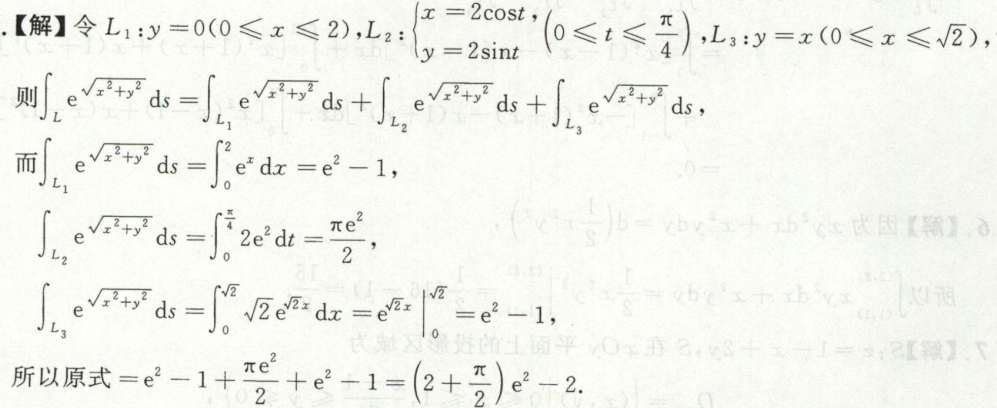
奇偶性对称性计算曲线积分
例1
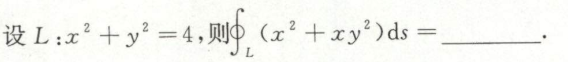
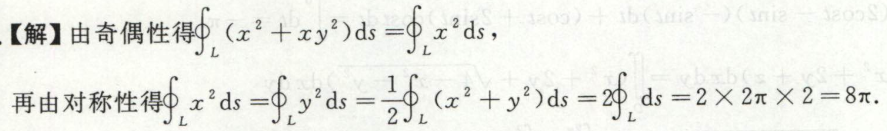
替换法计算曲线积分
例1

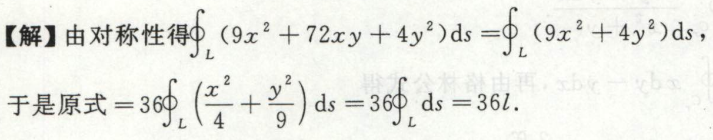
空间中对弧长的曲线积分
奇偶性对称性计算曲线积分
例1
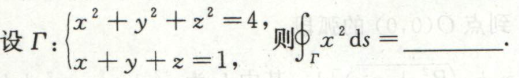

对坐标的曲线积分
平面上对坐标的曲线积分
定积分法计算曲线积分
例1


例2
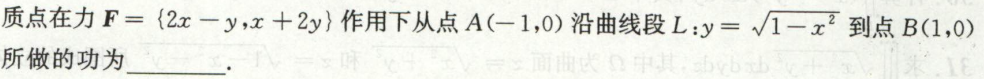
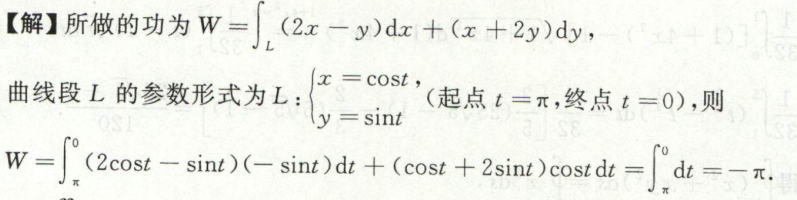
例3

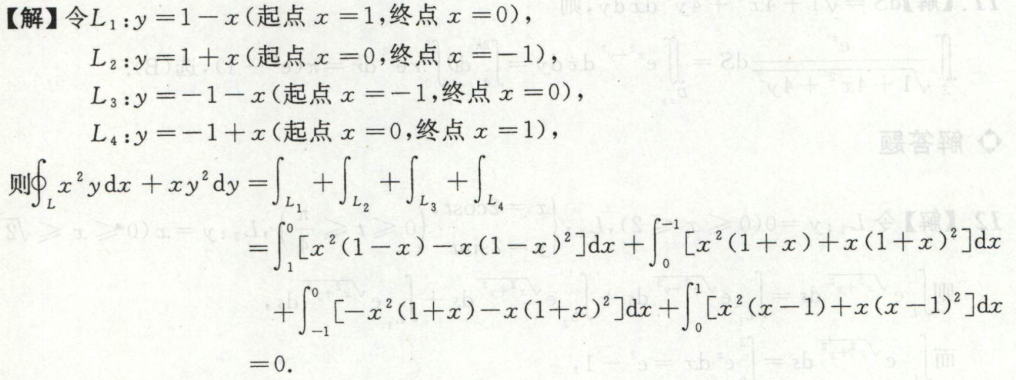
此题也可以用(格林公式法)将平面上的曲线积分转换为二重积分的方法来做。
例4


例5
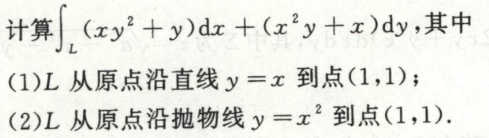
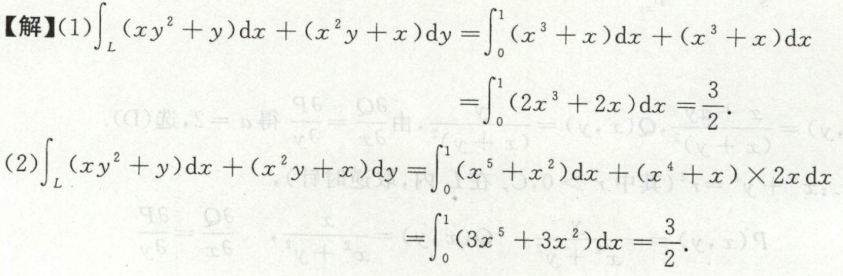
此题也可通过直观判断\(\\left(x y^{2}+y\\right) d x+\\left(x^{2} y+x\\right) d y = d(\\frac{1}{2} x^2 y^2 +xy)\),能写成全微分形式,得到该曲线积分与路径无关的结论,然后利用与路径无关的曲线积分计算方式来做。
例6
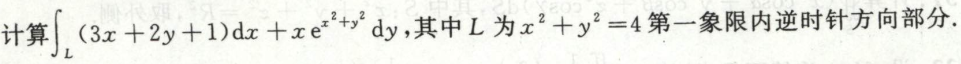

例7

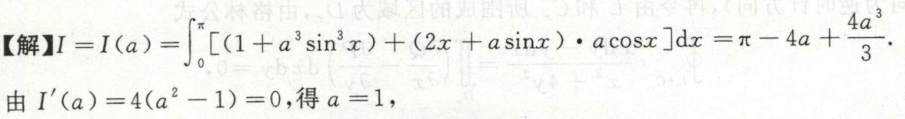
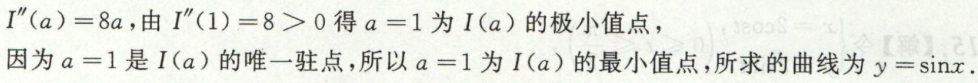
平面上曲线积分转换为二重积分(格林公式法)
例1

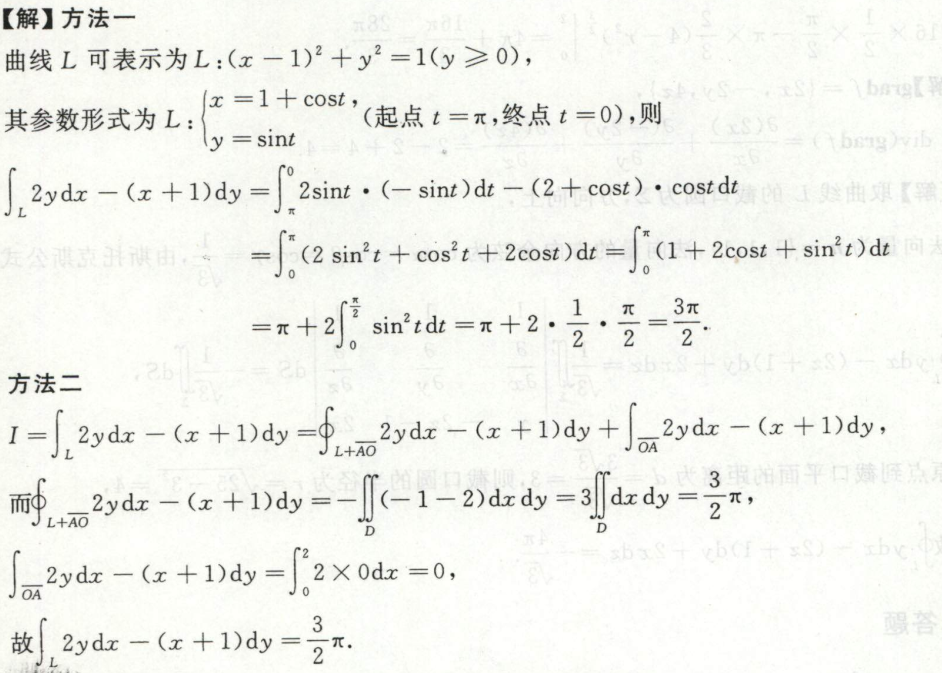
例2


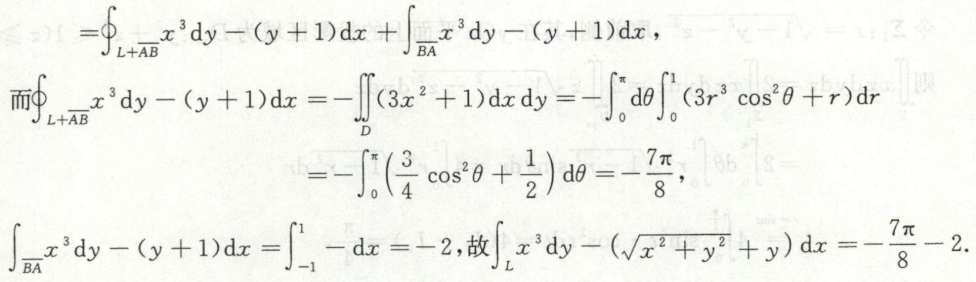
例3
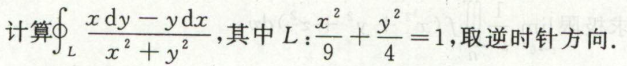

例4
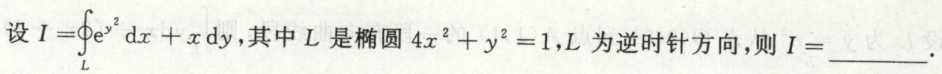

例5



例6
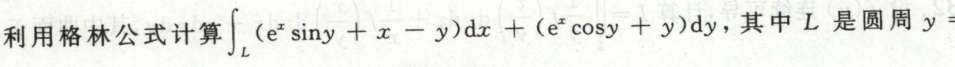
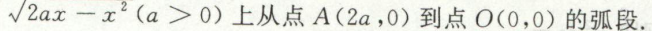

例7

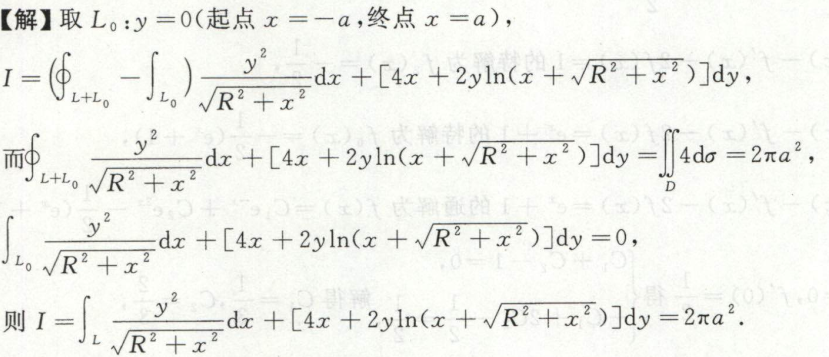
例8
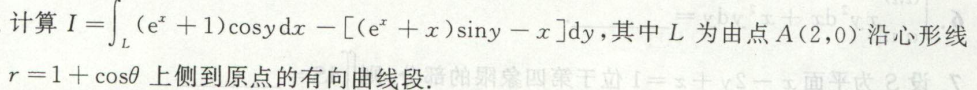

例9



例10


计算与积分路径无关的曲线积分
例1
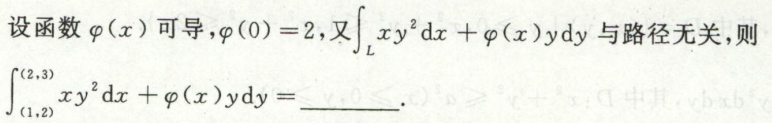

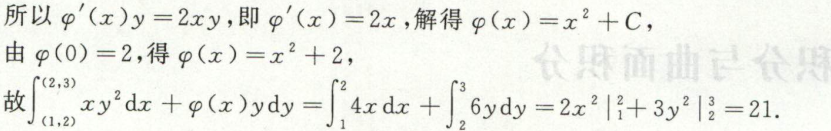
例2

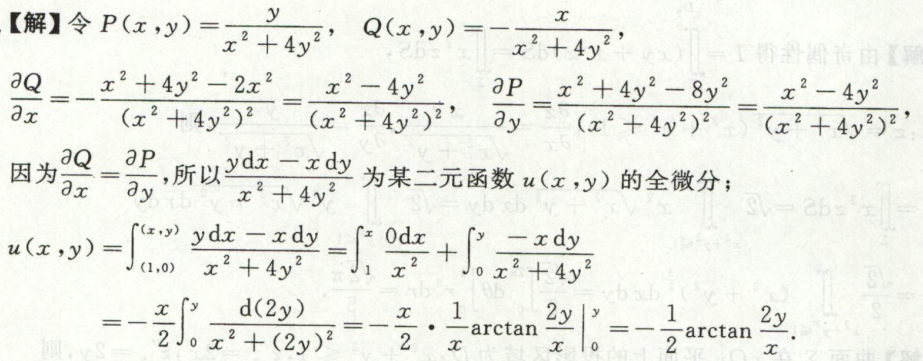
例3
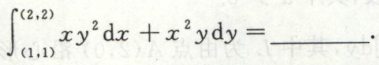
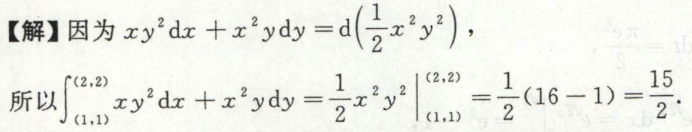
例4


例5
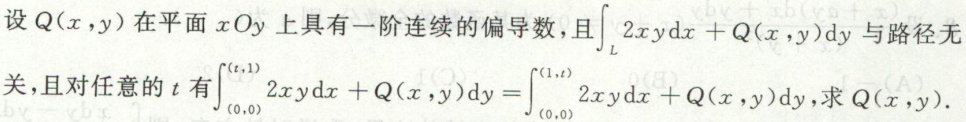

例6

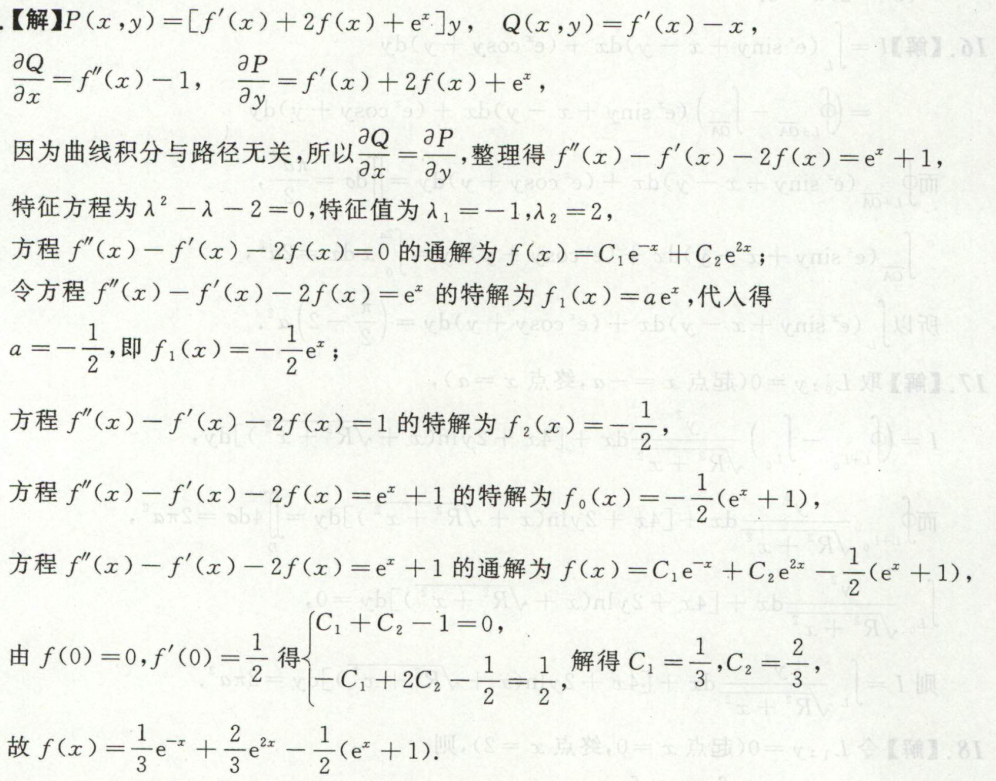
对面积的曲面积分
转换为二重积分法
例1
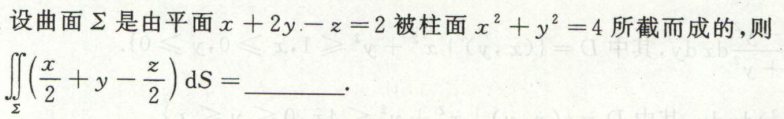
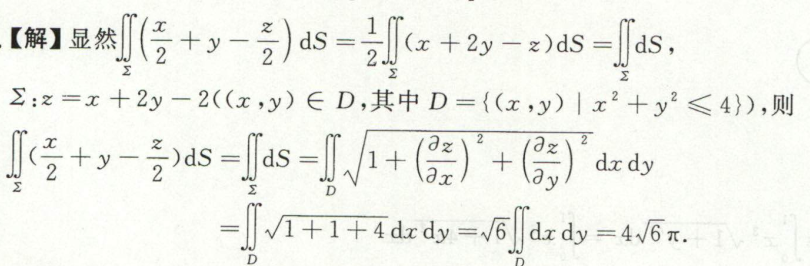
例2
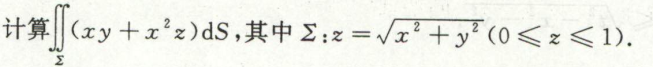
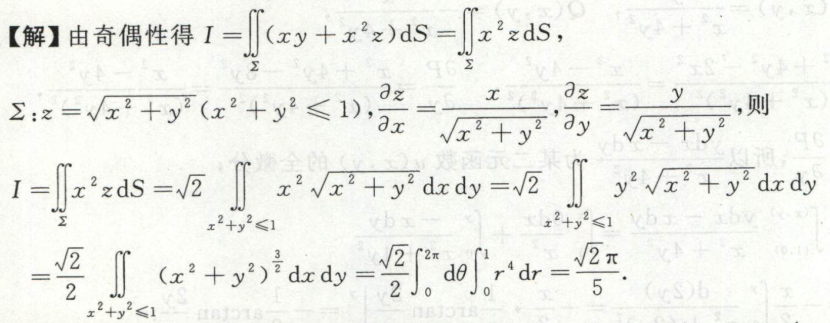
例3
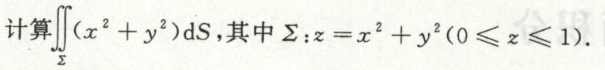
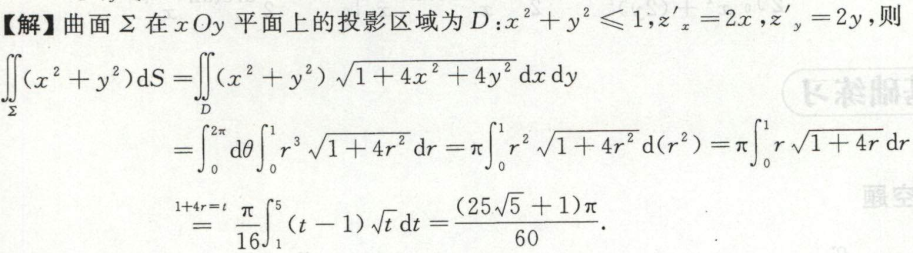
例4


提示:该平面写成截距式,易得在3个坐标轴上的截距分别为\(1,-\\frac{1}{2} ,1\)
例5

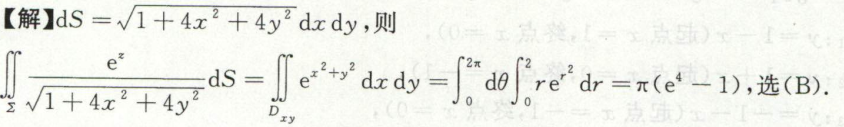
例6


例7

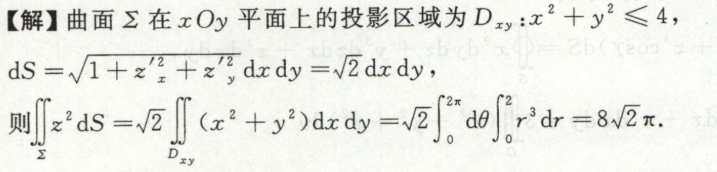
例8
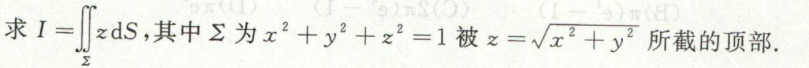

例9
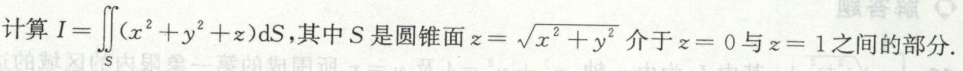
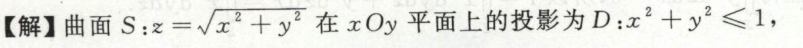
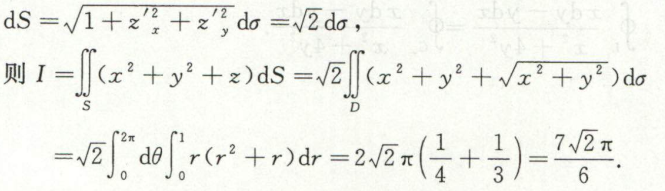
例10

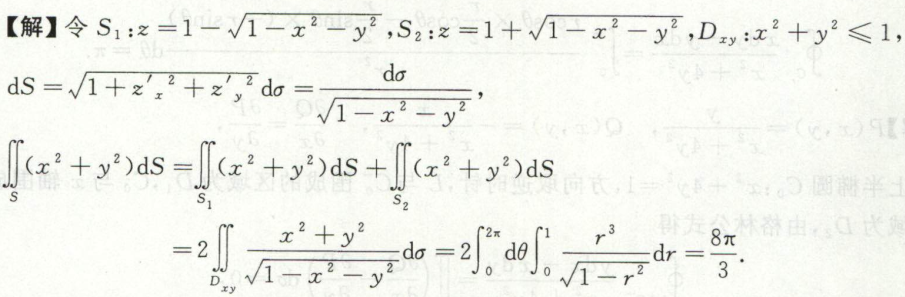
例11
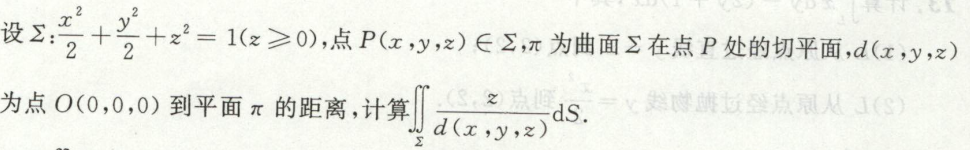
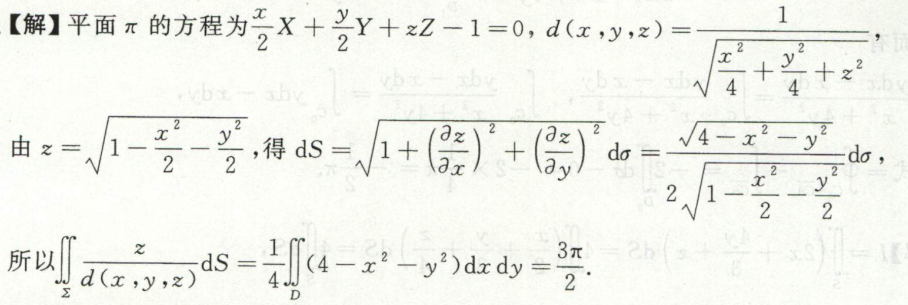
奇偶性对称性计算曲面积分
例1


提示:\(\\iint\_{\\Sigma} z \\mathrm{d} S = \\iint\_{\\Sigma} \\sqrt{1-x^2-y^2} \\mathrm{d} S= 4 \\iint\_{\\Sigma\_1} \\sqrt{1-x^2-y^2} \\mathrm{d} S = 4 \\iint\_{\\Sigma\_1} z \\mathrm{d} S = 4 \\iint\_{\\Sigma\_1} x \\mathrm{d} S\)
对坐标的曲面积分
转化为二重积分法
例1

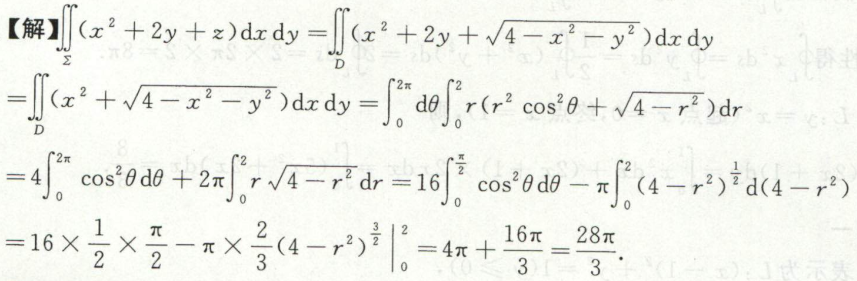
例2



注意:\(\\iint\_{\\Sigma} y^{2} \\mathrm{d} z \\mathrm{d} x = \\iint\_{\\Sigma} y^{2} \\cos\\beta dS\),显然\(\\cos\\beta\)是关于xOz是奇函数,可看出对称性
例3

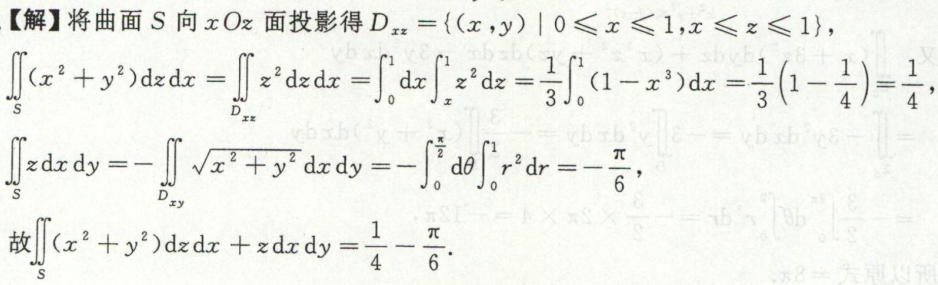
转换为三重积分法(高斯公式/空间内域与界的关系)
例1
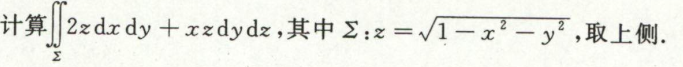
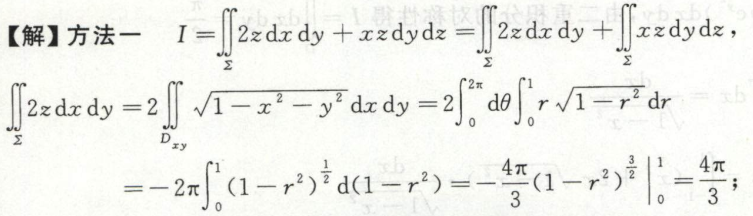

例2

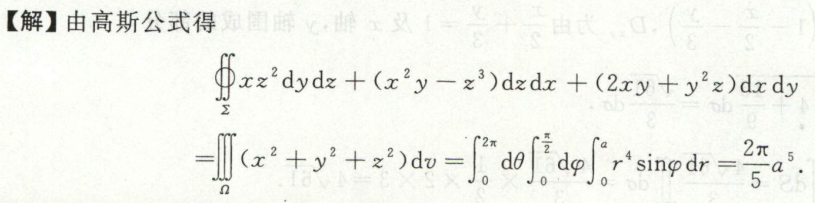
例3


例4 注意哈
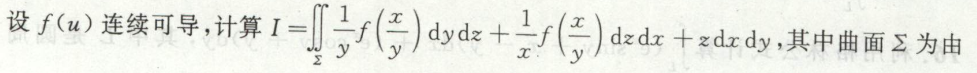
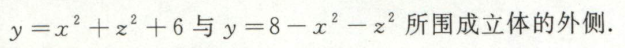

例5
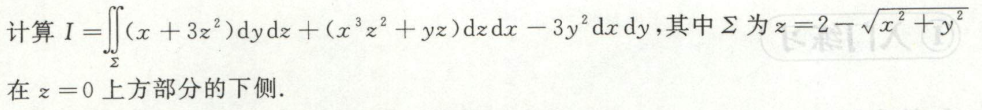

例6
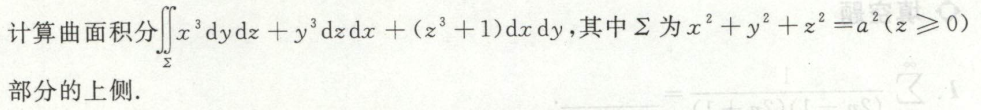
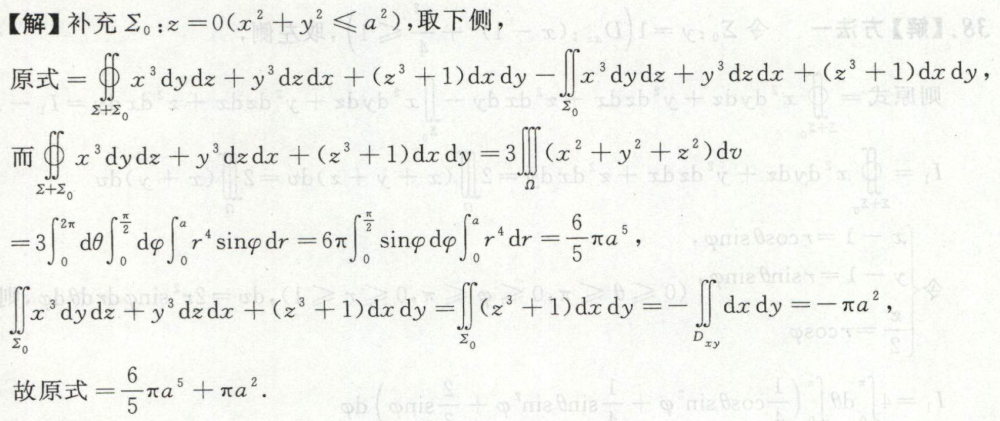
例7

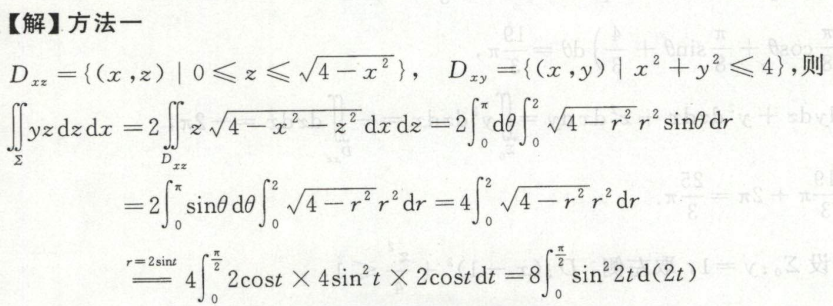
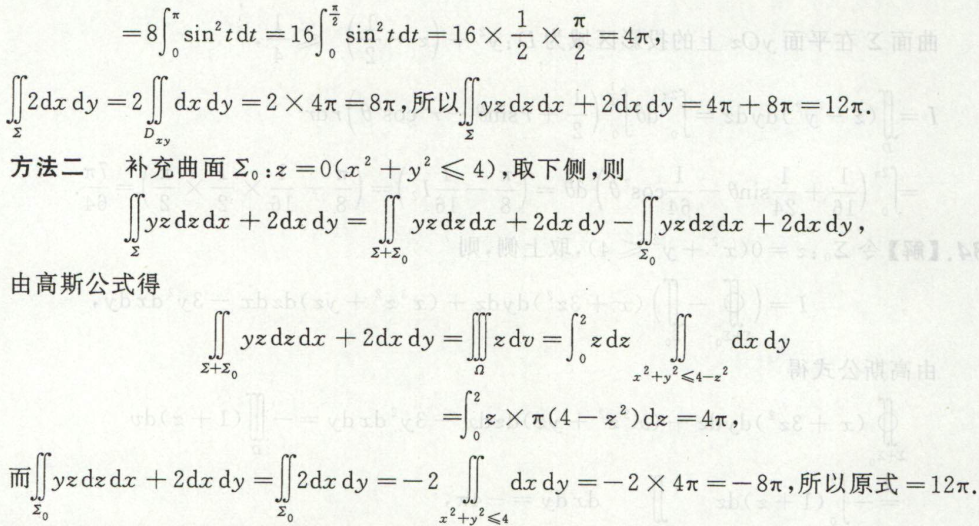
例8 嘿,脑细胞要死光了
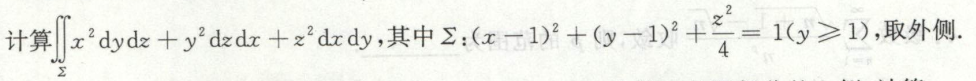


例9
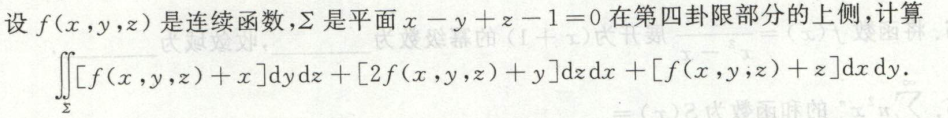

例10

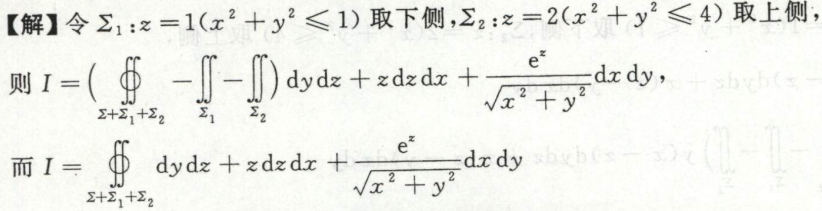
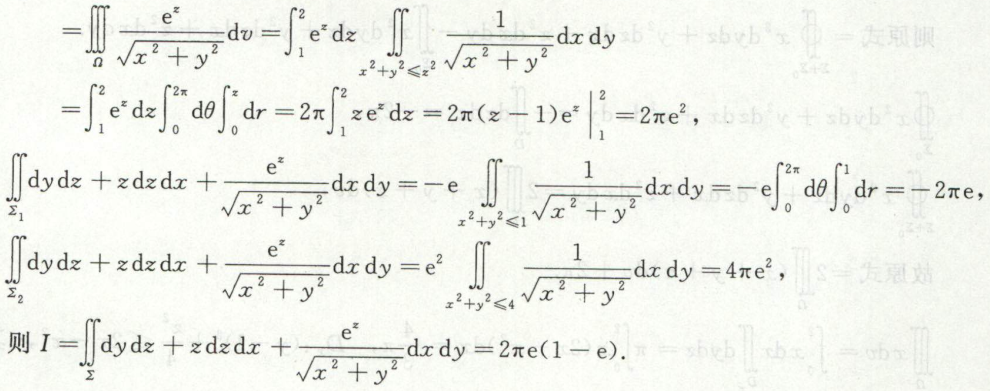
例11

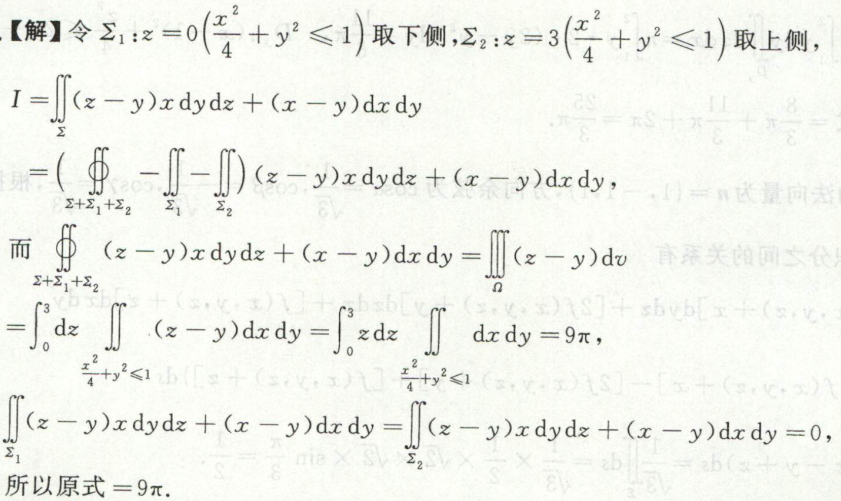
例12


例13

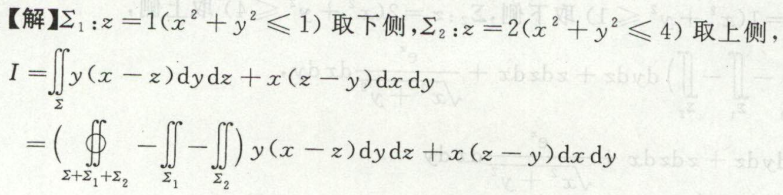
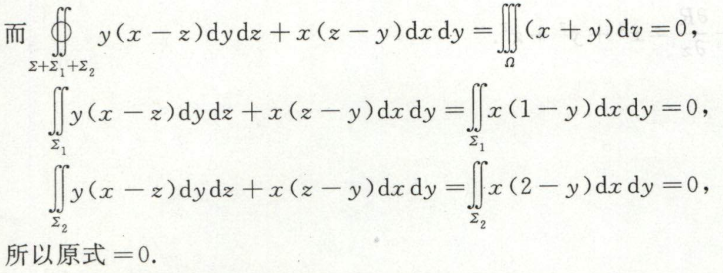
例14
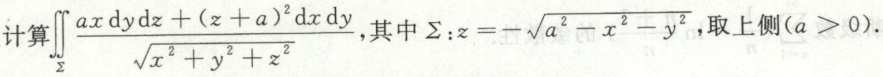

例15


转换为对面积的曲面积分
例1
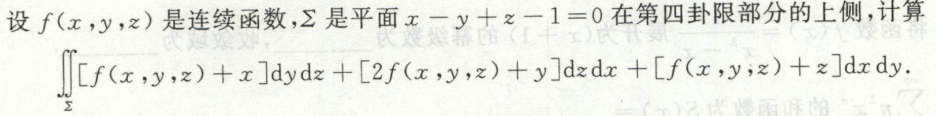
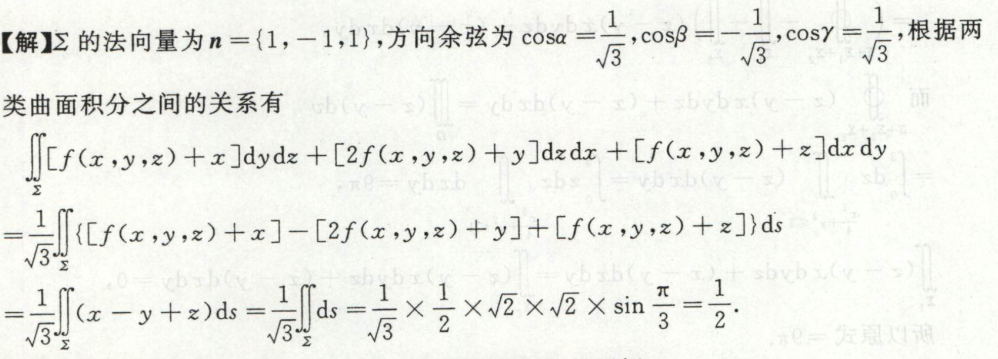
物理应用
散度
例1
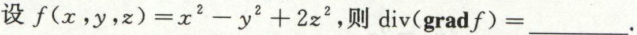
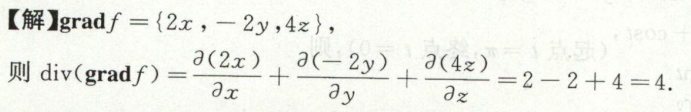
实际上\(\\operatorname{div}(\\operatorname{grad(f)})=\\nabla \\cdot(\\nabla f)= \\Delta f = \\frac{\\partial^2 f}{\\partial x^2}+\\frac{\\partial^2 f}{\\partial y^2}+\\frac{\\partial^2 f}{\\partial z^2}\),一般称为拉普拉斯算子
旋度
例1
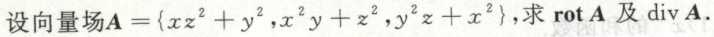
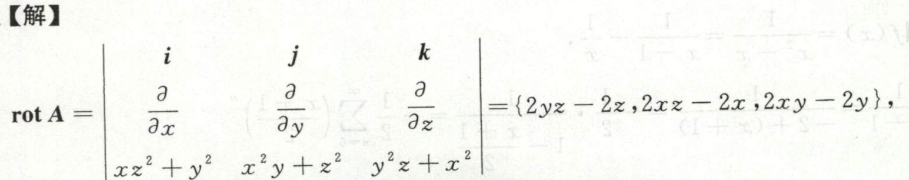
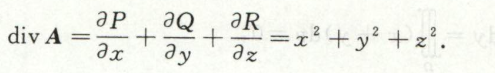
发表回复