Contents
高等数学-一元微分学-导数和微分
概念定理和公式
导数与微分定义
导数与可导定义
设函数\(y=f(x)\)在\(x\_0\)的邻域内有定义,\(f^{\\prime}\\left(x\_{0}\\right)=\\lim _{\\Delta x \\rightarrow 0} \\frac{\\Delta y}{\\Delta x}=\\lim _{\\Delta x \\rightarrow 0} \\frac{f\\left(x_{0}+\\Delta x\\right)-f\\left(x_{0}\\right)}{\\Delta x}\),称函数\(y=f(x)\)在点\(x\_0\)处可导,极限值称为函数的导数
还可以写成\(x \\rightarrow x\_0\)的等价定义(略)
由于导数是根据极限定义的。则 \(y=f(x)\)在\(x\_0\)处可导\(\\Leftrightarrow\) \(f\_{-}^{\\prime}\\left(x\_{0}\\right)\)和\(f\_{+}^{\\prime}\\left(x\_{0}\\right)\)存在且相等
左导数:\(f^{\\prime}_{-}\\left(x_{0}\\right)=\\lim _{\\Delta x \\rightarrow 0^{-}} \\frac{f\\left(x_{0}+\\Delta x\\right)-f\\left(x\_{0}\\right)}{\\Delta x}\)
右导数:\(f^{\\prime}_{+}\\left(x_{0}\\right)=\\lim _{\\Delta x \\rightarrow 0^{+}} \\frac{f\\left(x_{0}+\\Delta x\\right)-f\\left(x\_{0}\\right)}{\\Delta x}\)
导数几何意义
根据定义,导数是一个分式的极限,其中分子是函数在两点处的差值,分母是两点处的差值
函数在某点的导数,对应直角坐标系中曲线在该点处的斜率,即\(\\tan \\alpha=f^{\\prime}\\left(x\_{0}\\right)\)。
区间内可导与闭区间上可导
如果函数\(y=f(x)\)在\((a, b)\)内每一点均可导,称函数在\((a, b)\)内可导; 如果函数在\((a, b)\)内可导,且在x=a和x=b分别具有右导数\(f^{\\prime}+(a)\)和左导数\(f^{\\prime}-(b)\),则函数在\(\[a, b\]\)上可导。
微分与可微定义
如果函数y=f(x)在点x处的某邻域内有定义, \(\\Delta y=A \\Delta x+o(\\Delta x)\), 称y=f(x)在x处可微, 称\(d y=d f(x)=A \\Delta x\)为f(x)在x处的微分。
又\(f^{\\prime}(x)=\\lim \_{\\Delta x \\rightarrow 0} \\frac{\\Delta y}{\\Delta x}=A\),记\(d x=\\Delta x\),则微分又可以写成\(\\mathrm{d} y=f^{\\prime}(x) \\mathrm{d} x\)
导数与微分的重要定理与性质
(在某点处)导数存在 \(\\Leftrightarrow\) 左导数与右导数都存在且相等
(在某点处)可导 \(\\Rightarrow\) 连续
(在某点处)可微 \(\\Leftrightarrow\) 可导
(在某点及其邻域)可导(且导数不为0) \(\\Rightarrow\) 反函数可导,即\(\\frac{d x}{d y}=\\frac{1}{\\frac{d y}{d x}}\),即\(x^{\\prime} (y) = \\frac {1}{y^{\\prime}(x)}\)
\(d y=d f(x)=f^{\\prime}(x) d x\)
可导的偶函数的导数是奇函数;可导的奇函数的导数是偶函数。
导数与微分运算法则
设\(u=u(x), v=v(x)\)均可导,则:
\((1)(u \\pm v)^{\\prime}=u^{\\prime} \\pm v^{\\prime}, \\quad d(u \\pm v)=\\mathrm{d} u \\pm \\mathrm{d} v\) \((2)(w v)^{\\prime}=u v^{\\prime}+u u^{\\prime}, \\quad d(u v)=u \\mathrm{d} v+v \\mathrm{d} u\) \((u v w)^{\\prime}=u^{\\prime} v w+u v^{\\prime} w+u v w^\\prime\)
\((3)\\left(\\frac{u}{v}\\right)^{\\prime}=\\frac{u u^{\\prime}-u v^{\\prime}}{v^{2}}(v \\neq 0), \\mathrm{d}\\left(\\frac{u}{v}\\right)=\\frac{v \\mathrm{d} u-u \\mathrm{d} v}{v^{2}} \\quad(v \\neq 0)\)
导数公式与微分公式
| \(y=c\) | \(y^{\\prime}=0\) | \(d y=0\) |
|---|---|---|
| \(y=x^{\\alpha}\) | \(y^{\\prime}=a x^{\\alpha-1}\) | \(\\mathrm{d} y=\\alpha x^{\\alpha-1} \\mathrm{d} x\) |
| \(y=a^{x}\) | \(y^{\\prime}=a^{x} \\ln a\) | \(\\mathrm{d} y=a^{x} \\ln a d x\) |
| \(y=\\mathrm{e}^{x}\) | \(\\left(\\mathrm{e}^{z}\\right)^{\\prime}=\\mathrm{e}^{x}\) | \(\\mathrm{d}\\left(\\mathrm{e}^{x}\\right)=\\left\\langle\\mathrm{e}^{x}\\right\\rangle \\mathrm{d} x\) |
| \(y=\\log \_{a} x, a\>0, a \\neq 1\) | \(y^{\\prime}=\\frac{1}{x \\ln a}\) | \(d y=\\frac{1}{x \\ln a} d x \\quad(x\>0)\) |
| \(y=\\ln x\) | \((\\ln x)^{\\prime}=\\frac{1}{x}\) | \(d(\\ln x)=\\frac{1}{x} d x \\quad(x\>0)\) |
| \(y=\\sin x\) | \(y^{\\prime}=\\cos x\) | \(d(\\sin x)=\\cos x d x\) |
| \(y=\\cos x\) | \(y^{\\prime}=-\\sin x\) | \(\\mathrm{d}(\\cos x)=-\\sin x \\mathrm{d} x\) |
| \(y=\\tan x\) | \(y^{\\prime}=\\frac{1}{\\cos ^{2} x}=\\sec ^{2} x\) | \(\\mathrm{d}(\\tan x)=\\sec ^{2} x \\mathrm{d} x\) |
| \(y=\\cot x\) | \(y^{\\prime}=-\\frac{1}{\\sin ^{2} x}\) | \(d(\\cot x)=-\\csc ^{2} x d x\) |
| \(y=\\sec x\) | \(y^{\\prime}=\\sec x \\tan x\) | \(\\mathrm{d}(\\sec x)=\\sec x \\tan x \\mathrm{d} x\) |
| \(y=\\csc x\) | \(y^{\\prime}=-\\csc x \\cot x\) | \(d(\\csc x)=-\\csc x \\cot x d x\) |
| \(y=\\arcsin x\) | \(y^{\\prime}=\\frac{1}{\\sqrt{1-x^{2}}}\) | \(d(\\arcsin x)=\\frac{1}{\\sqrt{1-x^{2}}} d x\) |
| \(y=\\arccos x\) | \(y^{\\prime}=-\\frac{1}{\\sqrt{1-x^{2}}}\) | \(d(\\arccos x)=-\\frac{1}{\\sqrt{1-x^{2}}} d x\) |
| \(y=\\arctan x\) | \(y^{\\prime}=\\frac{1}{1+x^{2}}\) | \(d(\\arctan x)=\\frac{1}{1+x^{2}} d x\) |
| \(y=\\operatorname{arccot} x\) | \(y^{\\prime}=-\\frac{1}{1+x^{2}}\) | \(\\mathrm{d}(\\operatorname{arccot} x)=-\\frac{1}{1+x^{2}} \\mathrm{d} x\) |
高阶导数定义与基本公式
若y=f(x)的一阶导函数\(f^{\\prime}(x)\)在x点可导,称y=f(x)在x点存在二阶导函数\(f^{\\prime \\prime}(x)=\\lim \_{\\Delta x \\rightarrow 0} \\frac{f^{\\prime}(x+\\Delta x)-f^{\\prime}(x)}{\\Delta x}\)。
以此类推可得y=f(x)的n阶导函数\(f^{(n)}(x)=\\lim \_{\\Delta x \\rightarrow 0} \\frac{f^{(n-1)}(x+\\Delta x)-f^{(n-1)}(x)}{\\Delta x}\)
高阶导数公式
| \(\\left( x^{m}\\right)^{(n)}=m(m-1) \\cdot \\cdots \\cdot(m-n+1) x^{m-n}\) | |
|---|---|
| \(\\left(a^{x}\\right)^{(n)}=a^{x} \\ln ^{n} a\) | \(\\left(e^{x}\\right)^{(n)}=e^{z}\) |
| \((\\ln x)^{(n)}=(-1)^{n-1} \\frac{(n-1) !}{x^{n}}\) | |
| \((\\sin k x)^{(n)}=k^{n} \\sin \\left(k x+n \\cdot \\frac{\\pi}{2}\\right)\) | |
| \((\\cos k x)^{(n)}=k^{n} \\cos \\left(k x+n \\cdot \\frac{\\pi}{2}\\right)\) | |
| \((u v)^{(n)}=\\sum\_{i=0}^{n} C\_{n}^{i} u^{(i)} v^{(n-i)}\) | 即莱布尼兹高阶导数公式 |
| \(\\left(\\frac{1}{a x+b}\\right)^{(n)} =\\frac{(-1)^{n} m ! \\cdot a^{n}}{(a x+b)^{n+1}}\) | |
求各种函数的导数方法
求复合导数的微分
\(\\frac{d y}{d x}=\\frac{d y}{d u} \\cdot \\frac{d u}{d x}\)
求参数方程的导数和微分
\(\\frac{d y}{d x}=\\frac{y^{\\prime}(t)}{x^{\\prime}(t)}\)
\(\\begin{aligned} \\frac{\\mathrm{d}^{2} y}{\\mathrm{d} x^{2}} \&=\\frac{\\mathrm{d}}{\\mathrm{d} x}\\left(y^{\\prime}\\right)=\\frac{\\mathrm{d}}{\\mathrm{d} x}\\left(\\frac{y^{\\prime}(t)}{x^{\\prime}(t)}\\right)=\\frac{\\mathrm{d}}{\\mathrm{d} t}\\left(\\frac{y^{\\prime}(t)}{x^{\\prime}(t)}\\right) \\cdot \\frac{\\mathrm{d} t}{\\mathrm{d} x} \\ \&=\\frac{x^{\\prime}(t) y^{\\prime \\prime}(t)-y^{\\prime}(t) x^{\\prime \\prime}(t)}{\\left\[x^{\\prime}(t)\\right\]^{2}} \\cdot \\frac{1}{x^{\\prime}(t)}=\\frac{x^{\\prime}(t) y^{\\prime \\prime}(t)-y^{\\prime}(t) x^{\\prime \\prime}(t)}{\\left\[x^{\\prime}(t)\\right\]^{3}} \\end{aligned}\)
求隐函数的导数和微分
三种方法:
- 方程两边对x求导,注意y也是x的函数,方程两边分别作为复合函数求导
- 公式法:对于\(F(x, y)=0\),\(\\frac{\\mathrm{d} y}{\\mathrm{d} x}=-\\frac{F\_{x}^{\\prime}(x, y)}{F\_{y}^{\\prime}(x, y)}\)
- 方程两边取微分(微分形式不变性),然后解出\(\\frac{d y}{d x}\)
例2
由隐函数组成的参数方程求导

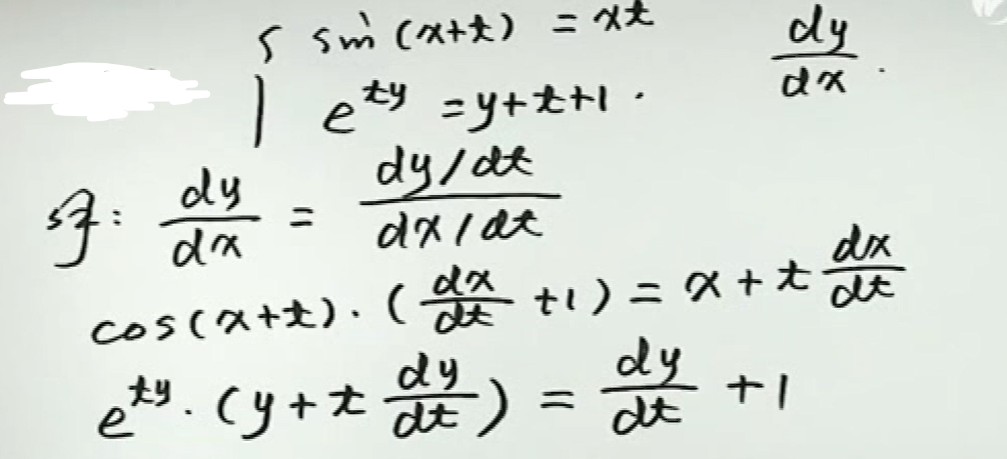
求幂指函数的导数和微分
\(y=u(x)^{v(x)} \\quad(u(x)\>0, u(x) \\neq 1) \\quad \\Rightarrow y=e^{v(x) \\ln u(x)}\)
\(y^{\\prime}=\\mathrm{e}^{\\mathrm{v}(x) \\ln x(x)}\\left\[v^{\\prime}(x) \\ln u(x)+v(x) \\cdot \\frac{u^{\\prime}(x)}{u(x)}\\right\]\)
\(=u(x)^{v(x)}\\left\[v^{\\prime}(x) \\ln u(x)+v(x) \\cdot \\frac{u^{\\prime}(x)}{u(x)}\\right\]\)
表达式为若干因子连乘、乘方、开方或商形式函数的导数或微分
一般用对数微分法(先对式子两边取对数,然后在等式的两边对x求导)
例: \(y=(x-2)^{2} \\sqrt\[3\]{\\frac{(x+3)^{2}\\left(3-2 x^{2}\\right)^{4}}{\\left(1+x^{2}\\right)\\left(5-3 x^{3}\\right)}}\),求y‘
先化为分式指数幂形式:\(y=(x-2)^{2}(x+3)^{\\frac{2}{3}}\\left(3-2 x^{2}\\right)^{\\frac{4}{3}}\\left(1+x^{2}\\right)^{-\\frac{1}{3}} \\cdot\\left(5-3 x^{3}\\right)^{-\\frac{1}{3}}\)
式子两边取对数:\(\\ln y=2 \\ln (x-2)+\\frac{2}{3} \\ln (x+3)+\\frac{4}{3} \\ln \\left(3-2 x^{2}\\right)-\\frac{1}{3} \\ln \\left(1+x^{2}\\right)-\\frac{1}{3} \\ln \\left(5-3 x^{3}\\right)\)
两边对x求导:\(\\frac{y^{\\prime}}{y}=\\frac{2}{x-2}+\\frac{2}{3(x+3)}-\\frac{16 x}{3\\left(3-2 x^{2}\\right)}-\\frac{2 x}{3\\left(1+x^{2}\\right)}+\\frac{3 x^{2}}{5-3 x^{3}}\)
代入y移项即可得最终结果
求分段函数的导数和微分
- 分段内与一般导数求法无异
- 分界点处的导数用导数的定义求
求绝对值函数的导数和微分
- 写成分段函数
- 求分段函数的导数和微分
求极限式表示的函数的导数和微分
- 先求极限,得到函数的分段表达式
- 求分段函数的导数和微分
求变限积分函数的导数和微分
如果函数\(f(x)\)在区间\(\[a,b\]\)连续,对于变上限积分函数\(\\Phi(x)=\\int\_{a}^{x} f(t) d t\),它的导数\(\\Phi^{\\prime}(x)=\\frac{d}{d x} \\int\_{a}^{x} f(t) d t=f(x)\),或者\(\\mathrm{d} \\Phi(x)=\\mathrm{d} \\int\_{a}^{x} f(t) \\mathrm{d} t=f(x) \\mathrm{d} x\)
如果函数\(f(x)\)在区间\(\[a,b\]\)连续,对于变下限积分函数\(\\Psi(x)=\\int\_{x}^{b} f(t) \\mathrm{d} t\),它的导数\(\\Psi^{\\prime}(x)=\\frac{d}{d x} \\int\_{x}^{b} f(t) d t=-f(x)\),或者\(\\Phi^{\\prime}(x)=\\frac{d}{d x} \\int\_{x}^{b} f(t) d t=-f(x)\)
如果函数\(f(x)\)在区间\(\[a,b\]\)连续,对于上下限都变的积分函数,它\(\\Phi(x)=\\int\_{g(x)}^{h(x)} f(t) d t\)的导数是\(\\Phi^{\\prime}(x)=f\[h(x)\] \\cdot h^{\\prime}(x)-f\[g(x)\] \\cdot g^{\\prime}(x)\)
高航 变限积分上求导:https://www.saikr.com/a/2774
讨论分界点处的导数和微分
求分段函数分界点的导数和微分
用导数的定义来看
带绝对值函数分界点的导数和微分
根据导数的定义来看(左右导数存在且相等)
例1


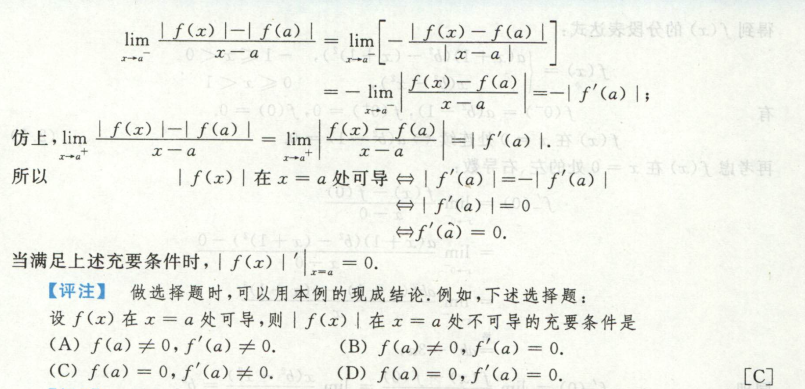
极限式表示的函数的可导性
- 先求极限,得到函数的的分段表达式
- 再讨论函数的可导性
例1

求高阶导数
- 直接法(归纳法):一阶,二阶,三阶,,,递推找规律
- 间接法(公式法):利用已知的高阶导数公式,通过四则运算,变量代换,泰勒级数等方法,达到将给定的函数求出n阶导数的方法,称之为间接法(//TODO 求高阶导数)
- 分式有理函数的高阶导数
- \(\\cos ^{n} \\alpha x, \\sin ^{m} \\beta x\)的和、差、积所构成的函数的高阶导数
- 利用函数的泰勤级数展开式,求函数在一点处的高阶导数
- 利用递推公式求n阶导数
- 利用莱布尼茨高阶导数公式求高阶导数
分式有理函数的高阶导数
- 先将有理假分式通过多项式除法化为整式与有理真分式之和,
- 再将有理真分式写成部分分式之和,
- 最后仿\(\\left(x^{m}\\right)^{(n)}\)的表达式写出所给定的有理函数的n阶导数
例1
\(y=\\frac{a x+b}{c x+d}\) 由多项式除法得:\(y=\\frac{a}{c}+\\frac{b c-a d}{c^{2}} \\frac{1}{x+\\frac{d}{c}}\) 将其有理真分式写成部分分式之和:\(y = \\frac{a}{c}+\\frac{b c-a d}{c^{2}}\\left(x+\\frac{d}{c}\\right)^{-1} \\quad\\left(x \\neq-\\frac{d}{c}\\right)\) 仿\(\\left(x^{m}\\right)^{(n)}\)求n阶导数: \(\\begin{aligned} y^{(n)} \&=\\frac{b c-a d}{c^{2}}(-1)(-2) \\cdots(-1-n+1)\\left(x+\\frac{d}{c}\\right)^{-1-n} \\ \&=\\frac{b c-a d}{c^{2}} \\frac{(-1)^{n} n !}{\\left(x+\\frac{d}{c}\\right)^{n+1}}=\\frac{(-1)^{n} n ! c^{n-1}(b c-a d)}{(c x+d)^{n+1}} \\end{aligned}\)
\(\\cos ^{n} \\alpha x, \\sin ^{m} \\beta x\)的和、差、积所构成的函数的高阶导数
利用三角函数中积化和差与倍角公式把函数的次数逐次降低,最后变为\(\\cos k x, \\sin k x\)的和、差形式,再用公式\(\\sin ^{(n)} k x=k^{n} \\sin \\left(k x+n \\cdot \\frac{\\pi}{2}\\right), \\cos ^{(n)} k x=k^{n} \\cos \\left(k x+n \\cdot \\frac{\\pi}{2}\\right)\)将给定函数的n阶导数写出来。
利用函数的泰勤级数展开式求高阶导数
例1

利用递推公式求高阶导数
//TODO
利用莱布尼茨公式求高阶导数
//TODO
已知导数求极限或参数,或者已知极限求导数
例1

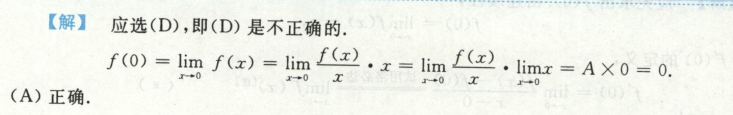

例2


导数与微分、增量的关系


发表回复