高等数学-级数

高等数学（数学分析）主要分为两块，微积分与级数。两者都建立在函数的极限理论之上。

级数是表示函数、研究函数性质以及数值计算的一种工具。函数可以展开成幂级数、三角级数的形式，级数也可以求其对应的和函数，因此把函数展开到级数形式可以研究函数的一些性质，也可以用级数计算函数。

常数项级数部分主要介绍级数的概念与一般性质。 函数项级数主要介绍幂级数、和三角级数（包括Fourier级数），着重讨论函数展开成幂级数、三角级数的问题，以及函数项级数表示成和函数的问题。

级数的基本概念与性质

级数的定义

高中我们已经学过数列。

简单的讲，无穷数列的和，就是级数。记为\(\\sum\_{n=1}^{\\infty} a\_n\)。 级数定义：给定一个无穷数列\(u\_{1}, u\_{2}, u\_{3}, \\cdots, u\_{n}, \\cdots\)，则\(\\sum\_{i=1}^{\\infty} u\_{i}=u\_{1}+u\_{2}+u\_{3}+\\cdots+u\_{i}+\\cdots\)称为级数，其中的第n项\(u\_n\)称为一般项。

当级数的各项\(a\_i\)都是常数时，形成的级数叫常数项级数； 当级数的各项\(a\_i\)都是关于x的函数时，形成的级数叫函数项级数。 当级数的各项\(a\_i\)都是复数时，形成的级数叫复数项级数；

类比研究反常积分的过程，研究反常要从正常开始，研究无限要从有限开始。 为了研究无限的级数，我们可以先看有限的部分和（前n项和）。 \(S\_n = a\_1 + a\_2 + a\_3 + … + a\_n\)，称为级数的部分和（前n项和）。

二重级数：给定带有两个下标i和j的无穷数集{aij}(i=1,2,…;j=1,2,…)，称记号a11+a12+…+a21+a22+…+a31+a32+…是二重级数(double series)。记作\(\\sum\_{m=1,n=1}^{\\infty} a\_{mn}\)，也可记作\(\\sum\_{m=1}^{\\infty} \\sum\_{n=1}^{\\infty} a\_{mn}\)，其中m，n各自独立地取正整数1，2，3，…

级数的收敛、发散、和的概念

如果\(\\Sigma\_{n=1}^{\\infty} a\_n = \\lim\_{n \\rightarrow \\infty} S\_n = S\)，称级数$\Sigma_{n=1}^{\infty} a_n \(**收敛**于S，这时S又称作级数\)\Sigma_{n=1}^{\infty} a_n $的和

如果\(\\Sigma\_{n=1}^{\\infty} a\_n\)的部分和\(\\lim\_{n \\rightarrow \\infty} S\_n\)不存在，称级数$\Sigma_{n=1}^{\infty} a_n $发散。

级数的性质

级数的四则运算性质

级数加减法、乘法，结果的收敛区间取原来两级数的收敛区间\((-R\_1, R\_1)\)和\((-R\_2,R\_2)\)中较小的一个. 级数的数乘不改变收敛区间， 级数的除法可能比原来两级数的收敛区间小得多（不做讨论）

级数的加减法性质（逐项相加、相减性质）

\(\\Sigma\_{n=1}^{\\infty} a\_n \\pm \\Sigma\_{n=1}^{\\infty} b\_n = \\Sigma\_{n=1}^{\\infty} (a\_n \\pm b\_n)\)

收敛级数的加减法：如果\(\\Sigma\_{n=1}^{\\infty} a\_n = A, \\Sigma\_{n=1}^{\\infty} b\_n = B\)，则\(\\Sigma\_{n=1}^{\\infty} (a\_n \\pm b\_n) = A \\pm B\)。即两个级数都收敛，和/差一定收敛。

另外有： 两个级数，一个发散，一个收敛，和/差一定发散。 两个级数，都发散，和/差的敛散性不确定。

级数的数乘性质

如果\(\\Sigma\_{n=1}^{\\infty} a\_n = S\)，则\(\\Sigma\_{n=1}^{\\infty} k a\_n = kS\)

也即\(k \\neq 0\)时，数乘级数敛散性不变。

级数加减数性质：改变级数的有限项，不改变级数敛散性

级数前[添加、减少、改变]有限项，不改变级数的敛散性

级数的乘法性质：柯西乘积

级数的乘法 \(\\left(\\sum\_{n=1}^{\\infty} u\_{n} \\right)\\cdot \\left(\\sum\_{n=1}^{\\infty} v\_{n}\\right)\)

柯西乘积：对于级数的乘法，若按“对角线法”排列结果，得\(u\_{1} v\_{1}+\\left(u\_{1} v\_{2}+u\_{2} v\_{1}\\right)+\\cdots+\\left(u\_{1} v\_{n}+u\_{2} v\_{n-1}+\\cdots+u\_{n} v\_{1}\\right)+\\cdots\)， 称此结果级数为两级数 \(\\sum\_{n=1}^{\\infty} u\_{n}\) 和 \(\\sum\_{n=1}^{\\infty} v\_{n}\) 的柯西乘积.（上面级数中括号内的作为一项） 注：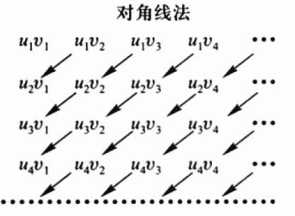

级数的除法性质

\(\\frac{a\_{0}+a\_{1} x+a\_{2} x^{2}+\\cdots+a\_{n} x^{n}+\\cdots}{b\_{0}+b\_{1} x+b\_{2} x^{2}+\\cdots+b\_{n} x^{n}+\\cdots}=c\_{0}+c\_{1} x+c\_{2} x^{2}+\\cdots+c\_{n} x^{n}+\\cdots\)，将左端分母乘到右边，右端变成级数乘法（柯西乘积），用待定系数法可确定系 数 \(c\_{0}, c\_{1}, c\_{2}, \\cdots, c\_{n}, \\cdots,\)

级数内添加括号可以提高收敛性

定理：如果级数 \(\\sum\_{n=1}^{\\infty} u\_{n}\) 收敛, 那么对这级数的项任意加括号后所成的级数$\left(u_{1}+\cdots+u_{n_{1}}\right)+\left(u_{n_{1}+1}+\cdots+u_{n_{2}}\right)+\cdots+\left(u_{n_{k-1}+1}+\cdots+u_{n_{k}}\right)+\cdots $仍收敛，且其和不变.

（其中每个括号对看作一项） （证明用到：数列极限性质：数列有极限，子列一定有极限）

原级数收敛，添加括号后的级数（更）收敛 如果级数添加括号后发散，那么原级数（更）发散

例1， 级数$ 1 – 1 + 1 – 1 +1 – 1 …\(发散，而级数\) (1 – 1) + (1 – 1) +(1 – 1) …$收敛

例2，如果\(\\Sigma\_{n=1}^{\\infty} a\_n\)收敛，则\(\\Sigma\_{n=1}^{\\infty} (a\_{2n-1} + a\_{2n}) = (a\_1 + a\_2) + (a\_3 + a\_4) + …\)收敛.

级数内添加绝对值可以提高发散性

级数收敛的必要条件（\(\\lim\_{n \\rightarrow \\infty} a\_n = 0\)）

如果\(\\Sigma\_{n=1}^{\\infty} a\_n\)收敛，则\(\\lim\_{n \\rightarrow \\infty} a\_n = 0\)。反之则不对。

证明：（无穷级数的证明，一般从有限的部分和证起） \(S\_n = a\_1 + a\_2 + a\_3 + … + a\_n\)， 因为\(\\Sigma\_{n=1}^{\\infty} a\_n\)收敛，所以\(\\lim\_{n \\rightarrow \\infty} S\_n = S\) 因为\(a\_n = S\_n – S\_{n-1}\)，则\(\\lim\_{n \\rightarrow \\infty} a\_n = \\lim\_{n \\rightarrow \\infty} S\_n – \\lim\_{n \\rightarrow \\infty} S\_{n-1} = S – S = 0\)。

级数收敛的充分必要条件（柯西审敛原理）

级数 \(\\sum\_{n=1}^{\\infty} u\_{n}\) 收敛的充分必要条件为 : 对于任意给定 的正数 \(\\varepsilon,\) 总存在正整数 \(N,\) 使得当 \(n\>N\) 时,对于任意的正整数 \(p\),都有\(\\left|u\_{n+1}+u\_{n+2}+\\cdots+u\_{n+p}\\right|\<\\varepsilon\)成立.

（用级数的和来证明，并用到：数列极限存在的柯西极限存在准则）

常数项级数

常数项级数的定义

级数的各项都是常数，则此级数就称为常数项级数。

两种重要的级数：p级数与几何级数

p级数和几何级数是两类比较重要的级数。其他级数审敛时，常用这两种级数作为参照级数。

p级数

级数\(\\Sigma\_{n=1}^{\\infty} \\frac{1}{n^p}\)称为p级数。

当\(p\>1\)时，级数\(\\Sigma \\frac{1}{n^p}\)收敛。 当\(p\\leq 1\)时，级数\(\\Sigma \\frac{1}{n^p}\)发散。

注：当\(p=1\)时，级数 \(\\Sigma \\frac{1}{n^p}= \\frac{1}{n}\)称为调和级数，此级数发散。（调和级数发散的证明用反证法：假设收敛于和S，证\(\\lim\_{n\\rightarrow \\infty} S\_{2n} – S\_{n} = \\frac{1}{n+1} + …+\\frac{1}{2n}\>\\frac{1}{2}\)，与\(\\lim\_{n\\rightarrow \\infty} S\_{2n} – S\_{n} = S – S = 0\)矛盾）

几何级数

级数\(\\Sigma\_{n=1}^{\\infty} a q^n (a \\neq 0 )\)称为几何级数

当\(|q|\<1\)时，几何级数$\Sigma_{n=1}^{\infty} a q^n \(收敛，收敛于\)\frac{a_1}{1-q}$ 当\(|q| \\ge 1\)时，几何级数$\Sigma_{n=1}^{\infty} a q^n $发散

正项级数与交错级数

数列各项都是非负常数，由此数列之和构成的级数叫做正项级数； 数列的项正负常数交错，由此数列之和构成的级数叫做交错级数。

下面单独分节讨论正项级数与交错级数

常数项级数：正项级数

正项级数的定义

\(\\Sigma\_{n=1}^{\\infty} a\_n \\quad (a\_n \\ge 0, n = 1,2,…)\)，称为正项级数

正项级数的性质

在一般级数的性质的基础上，正项级数还有如下性质：

正项级数的部分和是随n递增的，即\(S\_1 \\le S\_2 \\le S\_3 …\)

正项级数收敛的充分必要条件：它的部分和数列$ { s_n}\(有界. 即：正项级数的\)S_n\(无上界，则\)\lim_{n\rightarrow \infty} S_n = + \infty\(，即正项级数\)\Sigma_{n=1}^{\infty} a_n\(必发散于正无穷。正项级数的\)S_n\le M\(，则\)\lim_{n\rightarrow \infty} S_n \(存在，即正项级数\)\Sigma_{n=1}^{\infty} a_n$必收敛。

正项级数的审敛法

比较审敛法

比较审敛法基本形式

\(a\_n \\ge 0, b\_n \\ge 0\)， 1）当\(a\_n \\le b\_n\)，且\(\\Sigma\_{n=1}^{\\infty} b\_n\)收敛，则正项级数\(\\Sigma\_{n=1}^{\\infty} a\_n\)收敛。 2）当\(a\_n \\ge b\_n\)，且\(\\Sigma\_{n=1}^{\\infty} b\_n\)发散，则正项级数\(\\Sigma\_{n=1}^{\\infty} a\_n\)发散。

（推论：\(a\_n \\le k b\_n\)，且\(\\Sigma\_{n=1}^{\\infty} b\_n\)收敛，则正项级数\(\\Sigma\_{n=1}^{\\infty} a\_n\)收敛。）

（都由正项级数收敛的充分必要条件证明）

比较审敛法极限形式

\(a\_n \> 0, b\_n \> 0\)， 且\(\\lim\_{n \\rightarrow \\infty} \\frac{b\_n}{a\_n} = l \\quad (0\\le l\<+\\infty)\)，已知正项级数\(\\Sigma\_{n=1}^{\\infty} a\_n\)和的敛散性，则\(\\Sigma\_{n=1}^{\\infty} b\_n\)有相同的敛散性。

比值审敛法（达朗贝尔审敛法）

\(a\_n \> 0, \\quad \\lim\_{n \\rightarrow \\infty} \\frac{a\_{n+1}}{a\_n} = \\rho\) 1）$\rho <1 \(时，\)\Sigma_{n=1}^{\infty} a_n\(收敛。 2）\)\rho >1 \(时，\)\Sigma_{n=1}^{\infty} a_n\(发散。 3）\)\rho =1 \(时，\)\Sigma_{n=1}^{\infty} a_n$的敛散性不确定。

（此方法在含阶乘的级数中好用）

根值审敛法（柯西审敛法）

\(a\_n \> 0, \\quad \\lim\_{n \\rightarrow \\infty} \\sqrt\[n\]{a\_n} = \\rho\) 1）$\rho <1 \(时，\)\Sigma_{n=1}^{\infty} a_n\(收敛。 2）\)\rho >1 \(时，\)\Sigma_{n=1}^{\infty} a_n\(发散。 3）\)\rho =1 \(时，\)\Sigma_{n=1}^{\infty} a_n$的敛散性不确定。

（此方法在含n次幂的级数中好用）

极限审敛法

实际上是与p级数的比较，比较审敛法的极限形式

设 \(\\sum\_{n=1}^{\\infty} u\_{n}\) 为 正项级数， 1）如果 \(\\lim _{n \\rightarrow \\infty} n u_{n}=l\>0\\left(\\right.\) 或 \(\\left.\\lim _{n \\rightarrow \\infty} n u_{n}=+\\infty\\right)\)，那么级数 \(\\sum\_{n=1}^{\\infty} u\_{n}\) 发散； 2）如果 \(p\>1,\) 而 \(\\lim _{n \\rightarrow \\infty} n^{p} u_{n}=l(0 \\leqslant l\<+\\infty)\)，那么级数 \(\\sum\_{n=1}^{\\infty} u\_{n}\) 收敛.

常数项级数：交错级数

交错级数定义

\(\\Sigma\_{n=1}^{\\infty} (-1)^{n-1} a\_n = a\_1 – a\_2 + a\_3 – a\_4 …, \\quad a\_n \>0\)， 或者\(\\Sigma\_{n=1}^{\\infty} (-1)^{n} a\_n = – a\_1 + a\_2 – a\_3 + a\_4 …, \\quad a\_n \>0\)， 都称作交错级数

以上两种交错级数，实际上只差了一个常数\(k=-1\)，由级数性质可知，两级数敛散性相同。

交错级数的审敛

莱布尼兹法（Leibniz法）

设\(\\Sigma\_{n=1}^{\\infty} (-1)^{n-1} a\_n, \\quad a\_n \>0\)， 若\({a\_n}\)单调递减， 且\(\\lim\_{n \\rightarrow \\infty} a\_n = 0\)， 则交错级数\(\\Sigma\_{n=1}^{\\infty} (-1)^{n-1} a\_n, \\quad a\_n \>0\)收敛，且收敛位置\(S \\le a\_1\)，并有余项 \(r\_{n}\) 的绝对值 \(\\left|r\_{n}\\right| \\leqslant u\_{n+1}\)

eg1：\(\\Sigma\_{n=1}^{\\infty} \\frac{(-1)^n}{\\sqrt{n}}\)是否收敛？ 由于此交错级数的\(a\_n = \\frac{1}{\\sqrt{n}}\)，随n单调递减， 且\(\\lim\_{n \\rightarrow \\infty} a\_n = 0\)， 根据莱布尼兹审敛法可知，此交错级数\(\\Sigma\_{n=1}^{\\infty} \\frac{(-1)^n}{\\sqrt{n}}\)收敛

Q1：$\Sigma_{n=1}^{\infty} a_n \(收敛，\)\Sigma_{n=1}^{\infty} a_n^2 \(收敛吗？ A1：不一定，比如eg1中交错级数\)\Sigma_{n=1}^{\infty} \frac{(-1)^{n}{\sqrt{n}}\(收敛，但是调和级数\)\Sigma_{n=1}}{\infty} \frac{1}{n}$发散。

Q1：\(\\Sigma\_{n=1}^{\\infty} a\_n \\quad (a\_n \\ge 0)\)收敛，$\Sigma_{n=1}^{\infty} a_n^2 \(收敛吗？ A1：\)\Sigma_{n=1}^{\infty} a_n^2 \quad (a_n \ge 0) $一定收敛

条件收敛与绝对收敛

条件收敛定义

$\Sigma_{n=1}^{\infty} a_n \(收敛，而\)\Sigma_{n=1}^{\infty} |a_n| \(发散，称\)\Sigma_{n=1}^{\infty} a_n $条件收敛。

eg： \(1-\\frac{1}{2} +\\frac{1}{3} -\\frac{1}{4} …\)收敛， \(1 + \\frac{1}{2} + \\frac{1}{3} + \\frac{1}{4}…\)发散， 称上面的级数条件收敛。

绝对收敛定义

$\Sigma_{n=1}^{\infty} |a_n| \(收敛，称\)\Sigma_{n=1}^{\infty} a_n $绝对收敛。

注：级数内取绝对值号可以提高发散性。

绝对收敛级数的性质

（绝对收敛，无绝对值也收敛）如果级数 \(\\sum\_{n=1}^{\\infty} u\_{n}\) 绝对收敛,那么级数 \(\\sum\_{n=1}^{\\infty} u\_{n}\) 必定收敛.

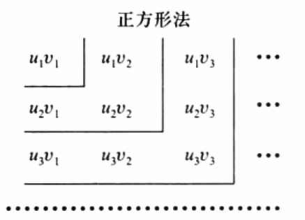
（绝对收敛级数具有可交换性 ）绝对收敛级数经改变项的位置后构成的级数也收敛,且与原级数有相同的和。（在二重级数、柯西乘积到正方形法级数乘积的转换种比较有用）

（绝对收敛级数的乘法）设级数 \(\\sum\_{n=1}^{\\infty} u\_{n}\) 和 \(\\sum\_{n=1}^{\\infty} v\_{n}\) 都绝对收敛 \(.\) 其和 分别为 \(s\) 和 \(\\sigma,\) 则它们的柯西乘积\(u\_{1} v\_{1}+\\left(u\_{1} v\_{2}+u\_{2} v\_{1}\\right)+\\cdots+\\left(u\_{1} v\_{n}+u\_{2} v\_{n-1}+\\cdots+u\_{n} v\_{1}\\right)+\\cdots\)也是绝对收敛的,且其和为 \(s\\sigma\)

注意柯西乘积（级数乘法）与二重积分（加法）的区别： 二重级数：给定带有两个下标i和j的无穷数集{aij}(i=1,2,…;j=1,2,…)，称记号a11+a12+…+a21+a22+…+a31+a32+…是二重级数(double series)。记作\(\\sum\_{m=1,n=1}^{\\infty} a\_{mn}\)，也可记作\(\\sum\_{m=1}^{\\infty} \\sum\_{n=1}^{\\infty} a\_{mn}\)，其中m，n各自独立地取正整数1，2，3，… 柯西乘积：按“对角线法”排列组成的级数\(u\_{1} v\_{1}+\\left(u\_{1} v\_{2}+u\_{2} v\_{1}\\right)+\\cdots+\\left(u\_{1} v\_{n}+u\_{2} v\_{n-1}+\\cdots+u\_{n} v\_{1}\\right)+\\cdots\)为两级数 \(\\sum\_{n=1}^{\\infty} u\_{n}\) 和 \(\\sum\_{n=1}^{\\infty} v\_{n}\) 的柯西乘积.记作 \(\\left(\\sum\_{n=1}^{\\infty} u\_{n} \\right)\\cdot \\left(\\sum\_{n=1}^{\\infty} v\_{n}\\right)\) 注：

函数项级数

函数项级数的定义

级数的项是函数构成的，称此级数为函数项级数。

函数项级数定义：如果给定一个定义在区间 I 上的函数列\(u\_{1}(x), u\_{2}(x), u\_{3}(x), \\cdots, u\_{n}(x), \\cdots,\)称为定义在区间 I 上的( 函数项)无穷级数,简称( 函数项) 级数.

对于每一个确定的值 \(x\_{0} \\in I,\) 函数项级数成为常数项级数\(u\_{1}\\left(x\_{0}\\right)+u\_{2}\\left(x\_{0}\\right)+u\_{3}\\left(x\_{0}\\right)+\\cdots+u\_{n}\\left(x\_{0}\\right)+\\cdots\)。当\(x=x\_0\)或者\(x\)暂时看作常数时，级数可看作常数项级数。即常数项级数的性质在函数项级数中仍可用。

函数项级数可能收敛也可能发散. 如果取\(x=x\_0\)时级数收敛, 就称点 \(x\_{0}\) 是函数项级数的收敛点 ; 如果取\(x=x\_0\)时级数发散, 就称点 \(x\_{0}\) 是函数项级数的发散点. 函数项级数的收敛点的全体称为它的收敛域, 发散点的全体称为它的发散域.

依照前面级数的相关概念：\(S\_n = a\_1 + a\_2 + a\_3 + … + a\_n\)，称为级数的部分和（前n项和）。如果\(\\Sigma\_{n=1}^{\\infty} a\_n = \\lim\_{n \\rightarrow \\infty} S\_n = S\)，称级数$\Sigma_{n=1}^{\infty} a_n \(**收敛**于S，这时S称作级数\)\Sigma_{n=1}^{\infty} a_n $的和。 对应于收敛域内的任意一个数 x,函数项级数成为一收剑的常数项级数,因而有一确定的和 s. 这样,在收敛域上, 函数项级数的和是 x 的函数 \(s(x)\)，通常称\(s(x)\) 为函数项级数的和函数

函数项级数的性质（未掌握）

函数项级数的每项都在区间上连续，函数项级数的和函数不一定在区间上连续。 函数项级数每一项的导数或积分之和 不一定等于和函数的导数或积分。

函数项级数的一致收敛定义

设有函数项级数 \(\\sum\_{n=1}^{\\infty} u\_{n}(x) .\) 如果对于任意给定的正数 \(\\varepsilon,\) 都存在着一个只依赖于 \(\\varepsilon\) 的正整数 \(N,\) 使得当 \(n\>N\) 时,对区间 I 上的一切 \(x\),都有不等式\(\\left|r\_{n}(x)\\right|=\\left|s(x)-s\_{n}(x)\\right|\<\\varepsilon\)成立,那么称函数项级数 \(\\sum\_{n=1}^{\\infty} u\_{n}(x)\) 在区间 \(I\) 上一致收敛于和 \(s(x),\) 也称函数序列 \(\\left{s\_{n}(x)\\right}\) 在区间 \(I\) 上一致收敛于 \(s(x) .\)

函数项级数一致收敛的充分条件

定理( 魏尔斯特拉斯( Weierstrass ) 判别法 ) \(\\quad\) 如果函数项级数 \(\\sum\_{n=1}^{\\infty} u\_{n}(x)\) 在 区间 I 上满足条件 : 1）\(\\left|u\_{n}(x)\\right| \\leqslant a\_{n}(n=1,2,3, \\cdots)\) 2）正项级数 \(\\sum\_{n=1}^{\\infty} a\_{n}\) 收敛 那么函数项级数 \(\\sum\_{n=1}^{\\infty} u\_{n}(x)\) 在区间 \(I\) 上一致收敛.

一致收敛的函数项级数的性质

定理 1（在区间上各项都连续、且一致连续的级数，其和函数也连续） \(\\quad\) 如 果 级 数 \(\\sum\_{n=1}^{\\infty} u\_{n}(x)\) 的 各 项区间 \(\[a, b\]\) 上 都 连 续，且\(\\sum\_{n=1}^{\\infty} u\_{n}(x)\) 在区间 \(\[a, b\]\) 上一致收敛于 \(s(x),\) 那么 \(s(x)\) 在 \(\[a, b\]\) 上也连续.

定理 2（在区间上各项都连续、且一致连续的级数，逐项可积） \(\\quad\) 如 果 级 数 \(\\sum\_{n=1}^{\\infty} u\_{n}(x)\) 的 各 项 \(u\_{n}(x)\) 在区间 \(\[a, b\]\) 上 连 续，且\(\\sum\_{n=1}^{\\infty} u\_{n}(x)\) 在 \(\[a, b\]\) 上一致收敛于 \(s(x),\) 那 么级数 \(\\sum\_{n=1}^{\\infty} u\_{n}(x)\) 在 \(\[a, b\]\) 上 可 以逐项 积分, 即\(\\int\_{x\_{0}}^{x} s(x) \\mathrm{d} x=\\int\_{x\_{0}}^{x} u\_{1}(x) \\mathrm{d} x+\\int\_{x\_{0}}^{x} u\_{2}(x) \\mathrm{d} x+\\cdots+\\int\_{x\_{0}}^{x} u\_{n}(x) \\mathrm{d} x+\\cdots\)其中 \(a \\leqslant x\_{0}\<x \\leqslant b,\) 并且上式右端的级数在[ \(\\left.a, b\\right\]\) 上也一致收敛。

定理 3 （在区间上各项都有连续导数、且一致连续的级数，逐项可导）\(\\quad\) 如果级数 \(\\sum\_{n=1}^{\\infty} u\_{n}(x)\) 在区间 \(\[a, b\]\) 上收敛于和 \(s(x)\). 它的各项 \(u\_{n}(x)\)都具有连续导数 \(u\_{n}^{\\prime}(x),\) 并且级数 \(\\sum\_{n=1}^{\\infty} u\_{n}^{\\prime}(x)\) 在 \(\[a, b\]\) 上一致收敛,那 么级数\(\\sum\_{n=1}^{\\infty} u\_{n}(x)\) 在 \(\[a, b\]\) 上也一致收敛,且可逐项求导,即\(s^{\\prime}(x)=u\_{1}^{\\prime}(x)+u\_{2}^{\\prime}(x)+\\cdots+u\_{n}^{\\prime}(x)+\\cdots\)

定理 4 （幂级数一定一致连续）\(\\quad\) 如果幂级数 \(\\sum\_{n=0}^{\\infty} a\_{n} x^{n}\) 的幂级数半径为 \(R\>0,\) 那么此级数在( \(\\left.-R, R\\right)\)内的任一闭区间[ a,b]上一致收敛.

定理 5 （幂级数可逐项求导，且收敛半径不变）如果幂级数 \(\\sum\_{n=0}^{\\infty} a\_{n} x^{n}\) 的收敛半径为 \(R\>0,\) 那么其和函数 \(s(x)\) 在\((-R, R)\) 内可导,且有逐项求导公式\(s^{\\prime}(x)=\\left(\\sum\_{n=0}^{\\infty} a\_{n} x^{n}\\right)^{\\prime}=\\sum\_{n=1}^{\\infty} n a\_{n} x^{n-1}\)逐项求导后所得到的幂级数与原级数有相同的收敛半径.

函数项级数：幂级数

相对于常数项级数，如果级数的项中含有函数，则称为函数项级数。 函数项级数取值，就变成了常数项函数。

幂级数属于函数项级数，是各项都是常数乘幂函数的函数项级数。

幂级数的定义

\(\\Sigma\_{n=0}^{\\infty} a\_n x^n = a\_0 + a\_1 x + a\_2 x^2 + …\) \(\\Sigma\_{n=0}^{\\infty} = a\_0 + a\_1 (x – x\_0) + a\_2 (x – x\_0)^2 + …\) 都称为幂级数。第二种可以通过换元变成第一种形式。

函数项级数取值，就变成了常数项函数。（幂级数属于函数项级数）

eg：幂级数： \(\\Sigma\_{n=0}^{\\infty} a\_n x^n = 1 + x + x^2 + …\) 取\(x = \\frac{1}{2}\)， 则级数变为\(\\Sigma\_{n=0}^{\\infty} (\\frac{1}{2})^n\)，级数收敛，即\(x=\\frac{1}{2}\)是收敛点； 取\(x = 3\)，则级数变为\(\\Sigma\_{n=0}^{\\infty} 3^n\)，级数发散，即\(x=3\)是发散点。

函数项级数特别关注使级数收敛的点（收敛点），即所有收敛点的集合（收敛域）

幂级数的性质

在一般级数的性质的基础上，幂级数还有如下性质

阿贝尔定理（Abel）：收敛半径的存在性

如 果 级 数 \(\\sum\_{n=0}^{\\infty} a\_{n} x^{n}\) 在当\({x}=x\_{0} \\quad\\left(x\_{0} \\neq 0\\right)\) 时 收敛，那么适合不等式 I \(x|\<| x\_{0} \\mid\) 的一切 \(x\) 使这幂级数绝对收敛. 反之,如果级数$\sum_{n=0}^{\infty} a_{n} x^{n} \(在当\)x = x_{0}$ 时发散，那么适合不等式 | \(x|\>| x\_{0} \\mid\) 的一切 \(x\) 使 这 幂级数发散。

推论（收敛半径一定存在）：对于幂级数\(\\Sigma\_{n=0}^{\\infty} a\_n x^n\)，存在\(R \\ge 0\)， 1）当\(|x| \< R\)，或者\(-R \< x \< R\)时，幂级数绝对收敛。 2）当$|x| >R \(时，幂级数发散。 3）当\)|x| = R$时，幂级数的收敛性不确定，需要具体分析。

收敛半径R的计算定理

对于幂级数$\Sigma_{n=0}^{\infty} a_n x^n $ 若\(\\lim\_{n \\rightarrow \\infty} \\left|\\frac{a\_{n+1}}{a\_n} \\right| = \\rho\)或者\(\\lim\_{n \\rightarrow \\infty} \\sqrt\[n\]{|a\_n|} = \\rho\)， 则： 1）当\(\\rho = 0\)时，收敛半径\(R = + \\infty\) （处处收敛） 2）当\(\\rho = +\\infty\)时，收敛半径\(R = 0\) （只有收敛点\(x=0\)） 3）当\(0\<\\rho\<+\\infty\)时，收敛半径\(R = \\frac{1}{\\rho}\)

注：对于收敛域的计算，除了计算收敛半径，还需要讨论一下两个边界是否收敛。

eg1：\(\\Sigma\_{n=0}^{\\infty} n! x^n\)的收敛半径R、收敛域？ \(\\lim\_{n \\rightarrow \\infty} \\left| \\frac{a\_{n+1}}{a\_n} \\right| = \\lim\_{n \\rightarrow \\infty} (n+1) = + \\infty\) 则收敛半径R=0，收敛域{0}

eg2：\(\\Sigma\_{n=0}^{\\infty} \\frac{x^n}{n!}\)的收敛半径R、收敛域？ \(\\lim\_{n \\rightarrow \\infty} \\left| \\frac{a\_{n+1}}{a\_n} \\right| = \\lim\_{n \\rightarrow \\infty} \\frac{1}{n+1} = 0\) 则此幂级数的收敛半径\(R=+\\infty\)，收敛域\((-\\infty, +\\infty)\)

eg3：$\Sigma_{n=0}^{\infty} \frac{x^n}{2n \cdot n} $的收敛半径R、收敛域？ $\lim_{n \rightarrow \infty} \left| \frac{a_{n+1}}{a_n} \right| = \lim_{n \rightarrow \infty} \frac{2^n \cdot n} {2^{n+1} \cdot (n+1)} = \frac{1}{2} $ 则此幂级数收敛半径R=2. 当\(x=-2\)时，级数变为\(\\Sigma\_{n=0}^{\\infty} \\frac{(-2)^n}{2^n \\cdot n} = \\Sigma\_{n=0}^{\\infty} \\frac{(-1)^n}{n}\)，此级数收敛； 当\(x=2\)时，级数变为\(\\Sigma\_{n=0}^{\\infty} \\frac{2^n}{2^n \\cdot n} = \\Sigma\_{n=0}^{\\infty} \\frac{1}{n}\)，此级数发散； 综上，此幂级数的收敛域为\(\[-2,2)\)

幂级数的运算性质

级数的四则运算性质

幂级数的分析性质（微积分性质）

幂级数$\Sigma_{n=0}^{\infty} a_n x^n, \quad x \in (-R, R) \(，实际上可看作一个x的函数，称\)S(x) = \Sigma_{n=0}^{\infty} a_n x^n $为幂级数的和函数。

幂级数的逐项可导性

对于幂级数$\Sigma_{n=0}^{\infty} a_n x^n, \quad x \in (-R, R) \(， 有\)\left(\Sigma_{n=0}^{\infty} a_n x^n \right)^\prime = S^\prime (x) = \Sigma_{n=0}^{\infty} (a_n xⁿ⁾\prime = \Sigma_{n=0}^{\infty} n a_n x^{n-1}$ 且\(\\Sigma\_{n=0}^{\\infty} n a\_n x^(n-1)\)的收敛半径仍为R不变。（但是端点处的收敛性可能发生变换，所以收敛域也可能发生变化）

幂级数的逐项可积性

对于幂级数$\Sigma_{n=0}^{\infty} a_n x^n, \quad x \in (-R, R) \(， 有\)\int_0^x \left( \Sigma_{n=0}^{\infty} a_n x^n\right) dx = \int_0^x S(x) dx = \Sigma_{n=0}^{\infty} \int_0^x a_n x^n dx = \Sigma_{n=0}^{\infty} \frac{a_n}{n+1} x^{n+1}$ 且\(\\Sigma\_{n=0}^{\\infty} \\frac{a\_n}{n+1} x^{n+1}\)的收敛半径仍为R不变。（但是端点处的收敛性可能发生变换，所以收敛域也可能发生变化）

幂级数的和函数必连续

幂级数 \(\\sum\_{n=0}^{\\infty} a\_{n} x^{n}\) 的和函数 \(s(x)\) 在其收敛域 \(I\) 上连续.

和函数和幂级数的互相变换

举例说明一下函数和级数的互换， \(\\Sigma\_{n=0}^{\\infty} x^n = \\frac{1}{1-x}, \\quad (-1\<x\<1)\)，左边到右边称为函数项级数求和函数。 \(\\frac{1}{1-x} = \\Sigma\_{n=0}^{\\infty} x^n, \\quad (-1\<x\<1)\)，左边到右边称为函数展开成级数。

函数展开成幂级数

直接法（公式法：泰勒级数、麦克劳林级数）

根据泰勒公式： 若\(f(x)\)在\(x\_0\)的邻域内\((n+1)\)阶可导， 则\(f(x)\)可展开到\((n+1)\)阶：\(f(x) = P\_n (x) + R\_n(x)\) \(P\_n(x) = f\\left(x\_{0}\\right)+\\frac{f^{\\prime}\\left(x\_{0}\\right)}{1 !}\\left(x-x\_{0}\\right)+\\frac{f^{\\prime \\prime}\\left(x\_{0}\\right)}{2 !}\\left(x-x\_{0}\\right)^{2}+\\cdots+\\frac{f^{(n)}\\left(x\_{0}\\right)}{n !}\\left(x-x\_{0}\\right)^{n}\)是主要部分， 余项可以写成：\(R\_{n}(x)=\\frac{f^{(n+1)}(\\xi)}{(n+1) !}\\left(x-x\_{0}\\right)^{n+1}\)称为拉格朗日余项， 余项也可以写成：\(R\_{n}(x)=o\\left(\\left(x-x\_{0}\\right)^{n}\\right)\)称为皮亚诺余项。

当\(f(x)\)可展开的阶数\((n+1) \\rightarrow \\infty\)时，有泰勒级数的概念： 若\(f(x)\)在\(x\_0\)的邻域内任意阶可导， 则\(f(x)\)可展开为级数： \(f(x) = \\Sigma\_{n=0}^{\\infty} \\frac{f^{(n)}(x\_0)}{n!} (x – x\_0)^n = f\\left(x\_{0}\\right)+\\frac{f^{\\prime}\\left(x\_{0}\\right)}{1 !}\\left(x-x\_{0}\\right)+\\frac{f^{\\prime \\prime}\\left(x\_{0}\\right)}{2 !}\\left(x-x\_{0}\\right)^{2}+\\cdots+\\frac{f^{(n)}\\left(x\_{0}\\right)}{n !}\\left(x-x\_{0}\\right)^{n}+…\)

定理（函数能展开称泰勒级数的充分必要条件）：设函数 \(f(x)\) 在点 \(x\_{0}\) 的某一邻域 \(U\\left(x\_{0}\\right)\) 内具有各阶导数 , 则 \(f(x)\) 在该 邻域内能展开成泰勒级数的充分必要条件是在该邻域内 \(f(x)\) 的泰勒公式中的余项 \(R\_{n}(x)\) 当 \(n \\rightarrow \\infty\) 时的极限为零,即\(\\lim _{n \\rightarrow \\infty} R_{n}(x)=0, x \\in U\\left(x\_{0}\\right)\)

直接法展开成泰勒级数的步骤：求函数各阶导，确认任意阶可导；写出泰勒级数，并确认余项趋于零\(\\lim _{n \\rightarrow \\infty} R_{n}(x)=0\)

当泰勒级数的展开位置\(x\_0 = 0\)时，相应的，叫做麦克劳林级数： 若\(f(x)\)在\(x\_0=0\)的邻域内任意阶可导， 则\(f(x)\)可展开为级数： \(f(x) = \\Sigma\_{n=0}^{\\infty} \\frac{f^{(n)}(0)}{n!} x^n = f\\left(0\\right)+\\frac{f^{\\prime}\\left(0\\right)}{1 !} x +\\frac{f^{\\prime \\prime}\\left(0\\right)}{2 !}x^{2}+\\cdots+\\frac{f^{(n)}\\left(0\\right)}{n !} x^{n}+…\)

常见函数的麦克劳林级数

函数	展开成麦克劳林级数（在\(x\_0=0\)附近展开成级数）	收敛域
\(e^x\)	\(=1+x+ \\frac{x^2}{2!} + … + \\frac{x^n}{n!} + ..\\ = \\Sigma\_{n=0}^{\\infty} \\frac{x^n}{n!}\)	\(-\\infty\<x\<+\\infty\)
\(\\sin x\)	\(= x – \\frac{x^3}{3!} + \\frac{x^5}{5!} – \\frac{x^7}{7!} +…\\ = \\Sigma\_{n=0}^{\\infty} \\frac{(-1)^n}{(2n+1)!} x^{2n+1}\)	\(-\\infty\<x\<+\\infty\)
\(\\cos x\)	\(=1 – \\frac{x^2}{2!} + \\frac{x^4}{4!} – \\frac{x^6}{6!} + … \\ = \\Sigma\_{n=0}^{\\infty} \\frac{(-1)^n}{(2n)!} x^{2n}\)	\(-\\infty\<x\<+\\infty\)
\(\\frac{1}{1-x}\)	\(=1+x+x^2+x^3+… \\ = \\Sigma\_{n=0}^{\\infty} x^n\)	\(-1\<x\<1\)
\(\\frac{1}{1+x}\)	\(= \\Sigma\_{n=0}^{\\infty} (-1)^n x^n\)	\(-1\<x\<1\)
\(ln(1+x)\)	\(=x-\\frac{x^2}{2} + \\frac{x^3}{3} – \\frac{x^4}{4} + … \\ = \\Sigma\_{n=1}^{\\infty} \\frac{(-1)^{n-1}}{n} x^n\) 注意这个级数从n=1开始	\(-1\<x \\le 1\)
\(-ln(1-x)\)	\(=x + \\frac{x^2}{2} + \\frac{x^3}{3} + \\frac{x^4}{4} + … \\ = \\Sigma\_{n=1}^{\\infty} \\frac{x^n}{n}\) 注意这个级数从n=1开始	\(-1 \\le x\<1\)
\((1+x)^{m}\)	\(=1+m x+\\frac{m(m-1)}{2 !} x^{2}+\\cdots+\\frac{m(m-1) \\cdots(m-n+1)}{n !} x^{n}+\\cdots\) 这个展开叫做二项展开式，也是代数学中的二项展开定理	\((-1\<x\<1)\)

间接法（借助常用麦克劳林展开、逐项可导、逐项可积性质）

间接法工具

常用函数的麦克劳林展开（在\(x\_0=0\)附近展开） 幂级数逐项可导性质 幂级数逐项可积性质

在指定位置附近展开成幂级数的例题：

eg1：将\(f(x) = \\frac{1}{x^2-1}\)展开成\((x-2)\)的幂级数 （或者说，在\(x\_0=2\)附近展开成幂级数） \(f(x)=\\frac{1}{2} \\left(\\frac{1}{x-1} -\\frac{1}{x+1}\\right)\) \(\\frac{1}{x-1} = \\frac{1}{1+(x-2)}= \\Sigma\_{n=0}^{\\infty} (-1)^n (x-2)^n , \\quad (-1\<x\<3)\) \(\\frac{1}{x+1} = \\frac{1}{3+(x-2)} = \\frac{1}{3} \\frac{1}{1+ \\frac{x-2}{3}} = \\frac{1}{3} \\Sigma\_{n=0}^{\\infty} (-1)^n \\left(\\frac{x-2}{3}\\right)^n = \\Sigma\_{n=0}^{\\infty} \\frac{(-1)^n}{3^{n+1}} (x-2)^n, \\quad (-1\<x\<5)\) 所以\(f(x) = \\Sigma\_{n=0}^{\\infty}\\frac{(-1)^n}{2} \\left(1-\\frac{1}{3^{n+1}}\\right)(x-2)^n, \\quad (1\<x\<3)\)

eg2：\(f(x) = \\frac{5x-1}{x^2-x-2}\)展成\((x-1)\)的幂级数（或者说，在\(x\_0=1\)附近展开成幂级数） \(f(x)=\\frac{5x-1}{(x-2)}= \\frac{A}{x+1} + \\frac{B}{x-2}, \\quad \\Rightarrow A = 2,B=3\) \(f(x) = 2 \\frac{1}{x+1} + 3 \\frac{1}{x-2}\) \(\\frac{1}{x+1} = \\frac{1}{2+(x-1)}= \\frac{1}{2} \\frac{1}{1+\\frac{x-1}{2}} = \\frac{1}{2} \\Sigma\_{n=0}^{\\infty} (-1)^n \\left(\\frac{x-1}{2}\\right)^2 = \\Sigma\_{n=0}^{\\infty} \\frac{(-1)^n}{2^{n+1}}(x-1)^n, \\quad (-1\<x\<3)\) \(\\frac{1}{x-2} = \\frac{1}{-1+(x-1)} = – \\frac{1}{1-(x-1)} = – \\Sigma\_{n=0}^{\\infty} (x-1)^n , \\quad (0\<x\<2)\) 所以\(f(x) = \\Sigma\_{n=0}^{\\infty} \\left\[ \\frac{(-1)^n}{2^n} – 3 \\right\] (x-1)^n, \\quad (0\<x\<2)\)

幂级数求和函数

幂级数求和函数工具

常见的麦克劳林展开 幂级数逐项可导性质 幂级数逐项可积性质

类型一：\(\\Sigma\_{n=0}^{\\infty} P(n) x^n\)求和函数

解法

幂级数逐项可导性质 麦克劳林级数\(\\Sigma\_{n=0}^{\\infty} x^n=\\frac{1}{1-x}, \\quad (-1\<x\<1)\) 麦克劳林级数\(\\Sigma\_{n=0}^{\\infty} (-1)^n x^n=\\frac{1}{1+x}, \\quad(-1\<x\<1)\)

eg1：给定幂级数$\Sigma_{n=1}^{\infty} n x^{n+1} \(,求其和函数\)S(x)$ 1）先求收敛域： \(\\lim\_{n \\rightarrow \\infty} \\left| \\frac{a\_{n+1}}{a\_n} \\right| = 1\)，得收敛半径\(R = 1\) 当\(x = \\pm 1\)时，\(n(-1)^{n+1} \\nrightarrow 1 (n \\rightarrow \\infty)\) 所以收敛域\((-1,1)\) 2）求和函数： \(S(x) = \\Sigma\_{n=1}^{\\infty} n x^{n+1} = x^2 \\Sigma\_{n=1}^{\\infty} n x^{n-1}\) \(=x^2 \\Sigma\_{n=1}^{\\infty} (x^n)^{\\prime} = x^2 x^2 \\left(\\Sigma\_{n=1}^{\\infty} x^n\\right)^{\\prime}\) \(=x^2 \\left(\\frac{x}{1-x}\\right)^{\\prime}\)

eg2：$\Sigma_{n=0}^{\infty} n^2 x^n \(， 求\)S(x)$

1）先求收敛域 $\lim_{n\rightarrow \infty} \left| \frac{a_{n+1}}{a_n} \right| = 1 $ 则收敛半径\(R = 1\) 当\(x= \\pm 1\)时，\(n^2 (\\pm 1) ^n \\nrightarrow 0 (n \\rightarrow \\infty)\) 所以收敛域\((-1,1)\) 2）求\(S(x)\) \(S(x) = \\Sigma\_{n=0}^{\\infty} n^2 x^n\) \(= \\Sigma\_{n=1}^{\\infty} n^2 x^n\) \(=\\Sigma\_{n=1}^{\\infty} \[n(n-1) +n\] x^n\) \(=\\Sigma\_{n=1}^{\\infty} n(n-1) x^n + \\Sigma\_{n=1}^{\\infty} n x^n\) \(=x^2 \\Sigma\_{n=1}^{\\infty} n(n-1) x^{n-2} + x\\Sigma\_{n=1}^{\\infty} n x^{n-1}\) \(=x^2 \\Sigma\_{n=1}^{\\infty} (x^n)^{\\prime\\prime} + x\\Sigma\_{n=1}^{\\infty} (x^n)^{\\prime}\) \(=x^2 \\left(\\Sigma\_{n=1}^{\\infty} x^n\\right)^{\\prime\\prime} + x \\left(\\Sigma\_{n=1}^{\\infty} x^n\\right)^{\\prime}\) （这里将括号内的幂级数，看作收敛的几何级数，几何级数的极限为\(\\frac{a\_1}{1-q}\)） \(=x^2 \\left(\\frac{x^2}{1-x} \\right)^{\\prime\\prime} + x \\left(\\frac{x}{1-x} \\right)^{\\prime}\)

类型二：\(\\Sigma\_{n=0}^{\\infty} \\frac{x^n}{P(n)}\)求和函数

解法

麦克劳林级数\(ln(1+x) = \\Sigma\_{n=1}^{\\infty} \\frac{(-1)^{n-1}}{n} x^n\)，注意这个级数从n=1开始 \((-1\<x \\le 1)\) 麦克劳林级数\(-ln(1-x) = \\Sigma\_{n=1}^{\\infty} \\frac{x^n}{n}\)注意这个级数从n=1开始 \((-1 \\le x \< 1)\) 麦消灭分母

eg1：\(\\Sigma\_{n=1}^{\\infty} \\frac{x^n}{n(n+1)}\),求和函数\(S(x)\) 1）先求收敛域 $\lim_{n\rightarrow\infty} \left| \frac{a_{n+1}}{a_n} \right| = 1 $ 此幂级数的收敛半径\(R = 1\) 当\(x = \\pm 1\)时，$\Sigma_{n=1}^{\infty} \frac{（\pm 1)^n}{n(n+1)} = \Sigma_{n=1}^{\infty} \frac{1}{n(n+1)} = 1 $ （用级数的定义法可证收敛于1：\(S\_n = \\frac{1}{1 \\times 2} + \\frac{1}{2 \\times 3} +… +\\frac{1}{n(n+1)}\)，则\(\\lim\_{n \\rightarrow \\infty} S\_n = 1\) ） 所以收敛域\(\[1,1\]\) 2）再求和函数\(S(x)\) \(\\begin{aligned} S(x) \&=\\sum\_{n=1}^{\\infty} \\frac{x^{n}}{n(n+1)} \\ \&=\\sum\_{n=1}^{\\infty} \\frac{x^{n}}{n}-\\sum\_{n=1}^{\\infty} \\frac{x^{n}}{n+1} \\end{aligned}\) 当\(x=0\)时，\(S(0) = 0\) 当\(x \\neq 0\)时， $\begin{aligned} S(x) &=-\ln(1-x)-\frac{1}{x} \sum_{n=1}^{\infty} \frac{x^{n+1}}{n+1} \ &=-\ln(1-x)-\frac{1}{x} \sum_{n=2}^{\infty} \frac{x^{n}}{n}\ &=-\ln (1-x)-\frac{1}{x}\left(\sum_{n=1}^{\infty} \frac{x^{n}}{n}-x\right) \ &=-\ln (1-x)-\frac{1}{x}[-\ln (1-x)-x] \ &=\left(\frac{1}{x}-1\right) \ln (1-x)+1 \end{aligned}, \quad(-1 \le x<1) and \quad x\neq 0 $ 当\(x=1\)时，\(S(1) = \\sum\_{n=1}^{\\infty} \\frac{1}{n(n+1)} =1\) 综上， \(f(x)=\\left{\\begin{array}{ll}0 \& , x=0 \\ 1 \& , x=1 \\ \\left(\\frac{1}{x}-1\\right) \\ln (1-x)+1, \& -1 \\leq x\<1,\\text{且} x \\neq 0\\end{array}\\right.\)

eg2：\(\\sum\_{n=0}^{\\infty} \\frac{(-1)^{n}}{2 n+1} x^{2 n}\), 求\(S(x)\) 1）先求收敛域： \(\\lim _{n \\rightarrow \\infty}\\left|\\frac{a_{n+1}}{a\_{n}}\\right|=1\) 得收敛半径\(R=1\) 且\(x= \\pm 1\)时，\(\\sum\_{n=0}^{\\infty} \\frac{(-1)^{n}}{2 n+1}\)收敛（交错级数单调递减，且\(\\lim\_{n\\rightarrow \\infty} a\_n =0\)，由莱布尼兹审敛法可得此级数收敛） 所以收敛域\(\[-1,1\]\) 2）再求\(S(x)\) 当\(x=0\)时，\(S(0) = 1\) 当\(x \\neq 0\)时，(下面步骤中将级数看作几何级数，几何级数收敛于\(\\frac{a\_1}{1-q}\),可以方便的转换成和函数的形式) \(\\begin{aligned} x S(x) \&=\\sum\_{n=0}^{\\infty} \\frac{(-1)^{n}}{2 n+1} x^{2 n+1} \\ \&=\\sum\_{i=0}^{\\infty}(-1)^{n} \\cdot \\int\_{0}^{x} x^{2 n} d x \\ \&=\\sum\_{n=0}^{\\infty} \\int\_{0}^{x}(-1)^{n} x^{n} d x \\ \&=\\int\_{0}^{x}\\left(\\sum\_{n=0}^{\\infty}(-1)^{n} x^{2 n}\\right) d x \\ \&=\\int\_{0}^{x}\\left(\\frac{1}{1+x^{2}}\\right) d x \\ \&=\\arctan x \\end{aligned}\) \((-1\<x^2 \\le 1)\)，即\((-1 \\le x \\le 1)\)

所以\(S(x) = \\frac{\\arctan x} {x}, \\quad (-1 \\le x \\le 1)\) 综上， \(S(x)=\\left{\\begin{array}{cc}1, \& x=0 \\ \\frac{a \\arctan x}{x}, \& -1 \\leq x \\leq 1 \\text { R } x \\neq 0\\end{array}\\right.\)

幂级数的应用

指数、对数、分数次幂、正余弦、定积分的近似计算

分数次幂的近似计算

eg1：计算 \(\\sqrt\[5\]{240}\) 的近似值,要求误差不超过 0.0001.

\(\\sqrt\[5\]{240}=\\sqrt\[5\]{243-3}=3\\left(1-\\frac{1}{3^{4}}\\right)^{1 / 5}\) 根据二项展开式\((1+x)^{m}=1+m x+\\frac{m(m-1)}{2 !} x^{2}+\\cdots+\\frac{m(m-1) \\cdots(m-n+1)}{n !} x^{n}+\\cdots\)，收敛域\((-1\<x\<1)\) 取\(m=\\frac{1}{5}, x=-\\frac{1}{3^{4}},\) 即得： \(\\begin{aligned} \\sqrt\[5\]{240}=3 \&\\left(1-\\frac{1}{5} \\cdot \\frac{1}{3^{4}}-\\frac{1 \\cdot 4}{5^{2} \\cdot 2 !} \\cdot \\frac{1}{3^{8}}-\\frac{1 \\cdot 4 \\cdot 9}{5^{3} \\cdot 3 !} \\cdot \\frac{1}{3^{12}}-\\cdots-\\right.\\ \&\\left.\\frac{1 \\cdot 4 \\cdot 9 \\cdot \\cdots \\cdot(5 n-6)}{5^{n} \\cdot n !} \\cdot \\frac{1}{3^{4 n}}-\\cdots\\right) \\end{aligned}\) 误差包括舍入误差和截断误差。 计算时保留到小数点后5位，首先保证舍入误差不超过 0.0001 取上式前两项时，截断误差（余项大小）： \(\\begin{aligned}\\left|r\_{2}\\right| \&=3\\left(\\frac{1 \\cdot 4}{5^{2} \\cdot 2 !} \\cdot \\frac{1}{3^{8}}+\\frac{1 \\cdot 4 \\cdot 9}{5^{3} \\cdot 3 !} \\cdot \\frac{1}{3^{12}}+\\frac{1 \\cdot 4 \\cdot 9 \\cdot 14}{5^{4} \\cdot 4 !} \\cdot \\frac{1}{3^{16}}+\\cdots\\right) \\ \&\<3 \\cdot \\frac{1 \\cdot 4}{5^{2} \\cdot 2 !} \\cdot \\frac{1}{3^{8}}\\left\[1+\\frac{1}{81}+\\left(\\frac{1}{81}\\right)^{2}+\\cdots\\right\] \\ \&=\\frac{6}{25} \\cdot \\frac{1}{3^{8}} \\cdot \\frac{1}{1-\\frac{1}{81}}=\\frac{1}{25 \\cdot 27 \\cdot 40}\<\\frac{1}{20000} \\end{aligned}\) 则取级数前两项时，得： \(\\sqrt\[5\]{240} \\approx 3\\left(1-\\frac{1}{5} \\cdot \\frac{1}{3^{4}}\\right) \\approx 2.9926\)

对数的近似计算

eg1：计算 ln 2 的近似值,要求误差不超过 0.000 1.

方法1： 有级数展开式：\(ln(1+x)=x-\\frac{x^2}{2} + \\frac{x^3}{3} – \\frac{x^4}{4} + … = \\Sigma\_{n=1}^{\\infty} \\frac{(-1)^{n-1}}{n} x^n \\quad (-1\<x \\leqslant 1)\) 假设取前n项作为近似值，由收敛的交错级数性质知，余项（正好是近似计算时的截断误差）： \(\\left|r\_{n}\\right| \\leqslant \\frac{1}{n+1}\) 需要取前10000项计算才能保证截断误差不超过 0.000 1. 下面找收敛更快的级数做近似计算

方法2： 级数展开式：\(\\ln (1+x)=x-\\frac{x^{2}}{2}+\\frac{x^{3}}{3}-\\frac{x^{4}}{4}+\\cdots+(-1)^{n-1} \\frac{x^{n}}{n}+\\cdots \\quad(-1\<x \\leqslant 1)\) x换为-x，得：\(\\ln (1-x)=-x-\\frac{x^{2}}{2}-\\frac{x^{3}}{3}-\\frac{x^{4}}{4}-\\cdots+(-1)^{n-1} \\frac{(-x)^{n}}{n}+\\cdots \\quad(-1 \\leqslant x\<1)\) 两式相减，只含奇数次幂： \(\\begin{aligned} \\ln \\frac{1+x}{1-x} \&=\\ln (1+x)-\\ln (1-x) \\\&=2\\left(x+\\frac{1}{3} x^{3}+\\frac{1}{5} x^{5}+\\cdots+\\frac{1}{2 n+1} x^{2 n+1}+\\cdots\\right)(-1\<x\<1) \\end{aligned}\) 令 \(\\frac{1+x}{1-x}=2,\) 解 出 \(x=\\frac{1}{3} .\) 以 \(x=\\frac{1}{3}\) 代 入： \(\\ln 2=2\\left(\\frac{1}{3}+\\frac{1}{3} \\cdot \\frac{1}{3^{3}}+\\frac{1}{5} \\cdot \\frac{1}{3^{5}}+\\frac{1}{7} \\cdot \\frac{1}{3^{7}}+\\cdots+\\frac{1}{2 n+1} \\cdot \\frac{1}{3^{2 n+1}}+\\cdots\\right)\) 取前四项，其截断误差（余项）为： \(\\begin{aligned}\\left|r\_{4}\\right| \&=2\\left(\\frac{1}{9} \\cdot \\frac{1}{3^{9}}+\\frac{1}{11} \\cdot \\frac{1}{3^{11}}+\\frac{1}{13} \\cdot \\frac{1}{3^{13}}+\\cdots+\\frac{1}{2 n+1} \\cdot \\frac{1}{3^{2 n+1}}+\\cdots\\right) \\ \&\<\\frac{2}{3^{11}}\\left\[1+\\frac{1}{9}+\\left(\\frac{1}{9}\\right)^{2}+\\cdots+\\left(\\frac{1}{9}\\right)^{n}+\\cdots\\right\] \\ \&=\\frac{2}{3^{11}} \\cdot \\frac{1}{1-\\frac{1}{9}}=\\frac{1}{4 \\cdot 3^{9}}\<\\frac{1}{70000} \\end{aligned}\) 计算时，取小数点后5位，首先保证舍入误差不超过 0.000 1. 则取级数前四项，得： \(\\ln 2 \\approx 2\\left(\\frac{1}{3}+\\frac{1}{3} \\cdot \\frac{1}{3^{3}}+\\frac{1}{5} \\cdot \\frac{1}{3^{5}}+\\frac{1}{7} \\cdot \\frac{1}{3^{7}}\\right)\\approx 0.6931\)

微分方程的幂级数解法

一阶微分方程的幂级数解法

一阶微分方程\(\\frac{\\mathrm{d} y}{\\mathrm{d} x}=f(x, y)\)，给定初值条件： \(\\left.y\\right|_{x=x_{0}}=y\_{0}\) 如果其中 函数 \(f(x, y)\) 是 \(\\left(x-x\_{0}\\right),\\left(y-y\_{0}\\right)\) 的多项式，即：\(f(x, y)=a\_{00}+a\_{10}\\left(x-x\_{0}\\right)+a\_{01}\\left(y-y\_{0}\\right)+\\cdots+a\_{l m}\\left(x-x\_{0}\\right)^{l}\\left(y-y\_{0}\\right)^{m}\)， 那么可设所求特解为：\(y=y\_{0}+a\_{1}\\left(x-x\_{0}\\right)+a\_{2}\\left(x-x\_{0}\\right)^{2}+\\cdots+a\_{n}\\left(x-x\_{0}\\right)^{n}+\\cdots\) 可用待定系数法求解其中系数 \(a\_{1}, a\_{2}, \\cdots, a\_{n}, \\cdots\)

eg1：求方程 \(\\frac{\\mathrm{d} y}{\\mathrm{d} x}=-y-x\) 满足 \(\\left.y\\right|\_{x=0}=2\) 的特解.

\(x\_{0}=0, y\_{0}=2\)，设方程的特解为\(y=2+a\_{1} x+a\_{2} x^{2}+\\cdots+a\_{n} x^{n}+\\cdots\) 则\(y^{\\prime}=a\_{1}+2 a\_{2} x+\\cdots+n a\_{n} x^{n-1}+\\cdots\) 代入方程得：\(a\_{1}+2 a\_{2} x+\\cdots+n a\_{n} x^{n-1}+\\cdots=-2-\\left(a\_{1}+1\\right) x-a\_{2} x^{2}-\\cdots-a\_{n} x^{n}-\\cdots\) 得\(a\_{1}=-2,2 a\_{2}=-\\left(a\_{1}+1\\right), 3 a\_{3}=-a\_{2}, \\cdots, n a\_{n}=-a\_{n-1}, \\cdots\) 得\(a\_{1}=-2\)，\(a\_{n}=(-1)^{n} \\frac{1}{n !}(n \\geqslant 2)\) 则微分方程得解为： \(\\begin{aligned} y \&=2-2 x+\\frac{1}{2 !} x^{2}-\\frac{1}{3 !} x^{3}+\\cdots+(-1)^{n} \\frac{1}{n !} x^{n}+\\cdots \\ \&=1-x+\\left\[1-x+\\frac{1}{2 !} x^{2}-\\frac{1}{3 !} x^{3}+\\cdots+(-1)^{n} \\frac{1}{n !} x^{n}+\\cdots\\right\] \\ \&=1-x+\\mathrm{e}^{-x} \\end{aligned}\)

二级齐次线性微分方程的幂级数解法

定理：如果二阶齐次线性微分方程\(y^{\\prime \\prime}+P(x) y^{\\prime}+Q(x) y=0\)中的系数 \(P(x)\) 与 \(Q(x)\) 可在 \(-R\<x\<R\) 内展开为 \(x\)的幂级数, 那么在 – \(R\<x\<R\) 内此方程必有形如\(y=\\sum\_{n=0}^{\\infty} a\_{n} x^{n}\)的解。

欧拉公式的证明

考察复数项级数\(1+z+\\frac{1}{2 !} z^{2}+\\cdots+\\frac{1}{n !} z^{n}+\\cdots \\quad(z=x+y i)\)， 可以证明这个复数项级数在整个复平面上是收敛的。 我们可以定义整个复平面上的复变量指数函数\(\\mathrm{e}^{z}=1+z+\\frac{1}{2 !} z^{2}+\\cdots+\\frac{1}{n !} z^{n}+\\cdots \\quad(|z|\<\\infty)\) 当 \(x=0\) 时, \(z\) 为纯虚数 \(y \\mathbf{i},\) 有： \(\\begin{aligned} \\mathrm{e}^{y\_{i}} \&=1+y \\mathrm{i}+\\frac{1}{2 !}(y \\mathrm{i})^{2}+\\frac{1}{3 !}(y \\mathrm{i})^{3}+\\cdots+\\frac{1}{n !}(y \\mathrm{i})^{n}+\\cdots \\ \&=1+y \\mathrm{i}-\\frac{1}{2 !} y^{2}-\\frac{1}{3 !} y^{3} \\mathrm{i}+\\frac{1}{4 !} y^{4}+\\frac{1}{5 !} y^{5} \\mathrm{i}-\\cdots \\ \&=\\left(1-\\frac{1}{2 !} y^{2}+\\frac{1}{4 !} y^{4}-\\cdots\\right)+\\left(y-\\frac{1}{3 !} y^{3}+\\frac{1}{5 !} y^{5}-\\cdots\\right) \\mathrm{i} \\ \&=\\cos y+\\mathrm{i} \\sin y \\end{aligned}\) 把 y 换写为 x,上式变为\(e^{x i}=\\cos x+i \\sin x\)，称为欧拉公式

函数项级数：三角级数

前面我们讨论了幂级数（以幂函数为项的级数）的概念、性质、函数展开成幂级数的条件与方法、求幂级数的收敛域以及和函数的方法。 类似的，我们想要讨论以三角函数系为各项组成的级数：三角级数\(\\sum\_{n=1}^{\\infty} A\_{n} \\sin \\left(n \\omega t+\\varphi\_{n}\\right)\)

三角级数的定义

\(A\_{1} \\sin \\left(\\omega t+\\varphi\_{1}\\right)+A\_{2} \\sin \\left(2 \\omega t+\\varphi\_{2}\\right)+…+A\_{n} \\sin \\left(n \\omega t+\\varphi\_{n}\\right)+…\) 即：\(\\sum\_{n=1}^{\\infty} A\_{n} \\sin \\left(n \\omega t+\\varphi\_{n}\\right)\) 习惯上会加个常数：\(A\_0 + \\sum\_{n=1}^{\\infty} A\_{n} \\sin \\left(n \\omega t+\\varphi\_{n}\\right)\) 通过三角函数的积化和差公式，并取\(2l = \\frac{2\\pi}{\\omega}\)可以变形为：\(\\frac{a\_{0}}{2}+\\sum\_{n=1}^{\\infty}\\left(a\_{n} \\cos \\frac{n \\pi t}{l}+b\_{n} \\sin \\frac{n \\pi t}{l}\\right)\) 再做变量代换\(\\frac{\\pi t}{l}=x\)得三角级数标准形式：\(\\frac{a\_{0}}{2}+\\sum\_{n=1}^{\\infty}\\left(a\_{n} \\cos n x+b\_{n} \\sin n x\\right)\)

设三角级数\(A\_0 + \\sum\_{n=1}^{\\infty} A\_{n} \\sin \\left(n \\omega t+\\varphi\_{n}\\right)\)收敛于\(f(t)\)，即\(f(t)=A\_0 + \\sum\_{n=1}^{\\infty} A\_{n} \\sin \\left(n \\omega t+\\varphi\_{n}\\right)\)。可以看出此三角级数是由一些周期为\(T\_n = \\frac{2 \\pi}{n \\omega}\)的正弦函数和常数\(A\_0\)的叠加，则\(f(t)\)是一个周期为\(T = \\frac{2 \\pi}{\\omega}\)的周期函数。 类似的，设三角级数\(\\frac{a\_{0}}{2}+\\sum\_{n=1}^{\\infty}\\left(a\_{n} \\cos n x+b\_{n} \\sin n x\\right)\)收敛于\(f(x)\)，即\(f(x)=\\frac{a\_{0}}{2}+\\sum\_{n=1}^{\\infty}\\left(a\_{n} \\cos n x+b\_{n} \\sin n x\\right)\)。可以看出此三角级数是一个周期\(T=2 \\pi\)的周期函数。

电工学谐波分析中，对于\(f(t)=A\_0 + \\sum\_{n=1}^{\\infty} A\_{n} \\sin \\left(n \\omega t+\\varphi\_{n}\\right)\)， 常数项 \(A\_0\)称为 \(f(t)\) 的直流分量, \(A\_{1} \\sin \\left(\\omega t+\\varphi\_{1}\\right)\) 称为一次谐波（或称基波）， \(A\_{2} \\sin \\left(2 \\omega t+\\varphi\_{2}\\right), A\_{3} \\sin \\left(3 \\omega t+\\varphi\_{3}\\right), \\cdots\) 依次称为二次谐波,三次谐波，等等。

三角函数系的正交性

三角函数系\(1, \\cos x, \\sin x, \\cos 2 x, \\sin 2 x, \\cdots, \\cos n x, \\sin n x, \\cdots\)在区间\(\[ -\\pi , \\pi \]\) 上正交，是指三角函数系中任意两个函数的乘积在区间\(\[ -\\pi , \\pi \]\) 上的积分等于0.

\(\\int\_{-\\pi}^{\\pi} \\cos n x \\mathrm{d} x=0 \\quad(n=1,2,3, \\cdots)\) \(\\int\_{-\\pi}^{\\pi} \\sin n x \\mathrm{d} x=0 \\quad(n=1,2,3, \\cdots)\) \(\\int\_{-\\pi}^{\\pi} \\sin k x \\cos n x \\mathrm{d} x=0 \\quad(k, n=1,2,3, \\cdots)\) \(\\int\_{-\\pi}^{\\pi} \\cos k x \\cos n x \\mathrm{d} x=0 \\quad(k, n=1,2,3, \\cdots, k \\neq n)\) \(\\int\_{-\\pi}^{\\pi} \\sin k x \\sin n x \\mathrm{d} x=0 \\quad(k, n=1,2,3, \\cdots, k \\neq n)\)

(用奇偶性对称性、三角函数的积化和差公式可证如上几个公式)

而三角函数系中，两个相同函数的乘积在区间 \(\[ – \\pi , \\pi \]\) 上的积分不等于0。

\(\\int\_{-\\pi}^{\\pi} 1^{2} \\mathrm{d} x=2 \\pi, \\int\_{-\\pi}^{\\pi} \\sin ^{2} n x \\mathrm{d} x=\\pi, \\int\_{-\\pi}^{\\pi} \\cos ^{2} n x \\mathrm{d} x=\\pi \\quad(n=1,2,3, \\cdots)\)

\(2\\pi\)周期的傅里叶级数

确定三角级数系数的方法

设 \(f(x)\) 是周期为 2 \(\\pi\) 的周期函数,且能展开成三角级数\(f(x)=\\frac{a\_{0}}{2}+\\sum\_{k=1}^{\\infty}\\left(a\_{k} \\cos k x+b\_{k} \\sin k x\\right)\)

利用三角函数系的正交性，如果级数逐项可积， 对原式两边取\(\[-\\pi,\\pi\]\)的定积分，移项可得\(a\_{0}=\\frac{1}{\\pi} \\int\_{-\\pi}^{\\pi} f(x) \\mathrm{d} x\)； 原式两边用乘以\(\\cos n x\)，然后取取\(\[-\\pi,\\pi\]\)的定积分，移项可得\(a\_{n}=\\frac{1}{\\pi} \\int\_{-\\pi}^{\\pi} f(x) \\cos n x \\mathrm{d} x \\quad(n=1,2,3, \\cdots)\) 原式两边用乘以\(\\sin n x\)，然后取取\(\[-\\pi,\\pi\]\)的定积分，移项可得\(b\_{n}=\\frac{1}{\\pi} \\int\_{-\\pi}^{\\pi} f(x) \\sin n x \\mathrm{d} x \\quad(n=1,2,3, \\cdots)\) 即可定出所有系数\(a\_{0}, a\_{1}, b\_{1}, \\cdots\)

\(2\\pi\)周期的傅里叶级数定义

如果三角级数\(f(x)=\\frac{a\_{0}}{2}+\\sum\_{k=1}^{\\infty}\\left(a\_{k} \\cos k x+b\_{k} \\sin k x\\right)\)逐项可积，可以用上面的公式定出所有的系数： \(\\left.\\begin{array}{ll}a\_{n}=\\frac{1}{\\pi} \\int\_{-\\pi}^{\\pi} f(x) \\cos n x \\mathrm{d} x \& (n=0,1,2,3, \\cdots) \\ b\_{n}=\\frac{1}{\\pi} \\int\_{-\\pi}^{\\pi} f(x) \\sin n x \\mathrm{d} x \&(n=1,2,3, \\cdots)\\end{array}\\right}\) 称三角级数\(\\frac{a\_{0}}{2}+\\sum\_{k=1}^{\\infty}\\left(a\_{k} \\cos k x+b\_{k} \\sin k x\\right)\)为\(f(x)\)的傅里叶级数。

函数展成傅里叶级数的充分条件

定理(收敛定理, 狄利克雷( Dirichlet) 充分条件 )设 \(f(x)\) 是周期为 2 \(\\pi\) 的周期函数,如果它满足： 1）在一个周期内连续或只有有限个第一类间断点， 2）在一个周期内至多只有有限个极值点， 那么 \(f(x)\) 的傅里叶级数收敛,并且： 当 \(x\) 是 \(f(x)\) 的连续点时,级数收敛于 \(f(x)\); 当 \(x\) 是 \(f(x)\) 的间断点时,级数收敛于 \(\\frac{1}{2}\\left\[f\\left(x^{-}\\right)+f\\left(x^{+}\\right)\\right\] .\)

（即：只要函数在\(\[ – \\pi，\\pi \]\)上至多有有限个第一类间断点,并 且不作无限次振动,函数的傅里叶级数在连续点处就收敛于该点的函数值,在间断点处收敛于该点左极限与右极限的算术平均值. ）

可见,函数展开成傅里叶级数的条件比展开成幂级数的条件低得多。

函数的延拓

周期延拓

如果函数 \(f(x)\) 只在 [ – \(\\pi, \\pi\]\) 上有定义,并且满足收敛定理的条外补充函数 \(f(x)\) 的定义,使它拓广成周期为 2 \(\\pi\) 的周期函数 F( x). 按这种方式 拓广函数的定义域的过程称为周期延拓.再将 F( x)展开成傅里叶级数. 最后限制 \(x\) 在( \(-\\pi, \\pi)\) 内,此时 \(F(x) \\equiv f(x),\) 这样便得到 \(f(x)\) 的傅里叶级数展开式. 根 据收剑定理,这级数在区间端点 \(x=\\pm \\pi\) 处收竣于 \(\\frac{f\\left(\\pi^{-}\\right)+f\\left(-\\pi^{+}\\right)}{2}\)

奇延拓或偶延拓

设函数 \(f(x)\)定义在区间\(\[0, \\pi \]\)上并且满足收敛定理的条件, 我们在开区间\(( – \\pi ,0 )\) 内补充函数 \(f(x)\) 的定义, 得到定义在\(( – \\pi, \\pi\]\) 上的函数 \(F(x),\) 使它在 \((-\\pi, \\pi)\) 上成为 奇函数(偶函数). 按这种方式拓广函数定义域的过程称为奇延拓(偶延拓)。 然后将奇延拓(偶延拓)后的函数展开成傅里叶级数,这个级数必定是正弦级数余弦级数）. 再限制 \(x\) 在 \((0, \\pi\]\) 上,此时 \(F(x) \\equiv f(x),\) 这样便得到 \(f(x)\) 的正弦级 数(余弦级数)展开式.

正弦级数和余弦级数

些函数的傅里叶级数只含有正弦项，这样的级数称为正弦级数。或者只含有常数项和余弦项，这样的级数称为余弦级数。

当 \(f(x)\) 为奇函数时 \(f(x) \\cos n x\) 是奇函数 \(, f(x) \\sin n x\) 是偶函数,故: \(\\left.\\begin{array}{l}a\_{n}=0 \\quad(n=0,1,2, \\cdots) \\ b\_{n}=\\frac{2}{\\pi} \\int\_{0}^{\\pi} f(x) \\sin n x \\mathrm{d} x \\quad(n=1,2,3, \\cdots)\\end{array}\\right}\) 即知奇函数的傅里叶级数是只含有正弦项的正弦级数\(\\sum\_{n=1}^{\\infty} b\_{n} \\sin n x\)

当 \(f(x)\) 为偶函数时 \(, f(x) \\cos n x\) 是偶函数 \(, f(x) \\sin n x\) 是奇函数,故: \(\\left.\\begin{array}{l}a\_{n}=\\frac{2}{\\pi} \\int\_{0}^{\\pi} f(x) \\cos n x \\mathrm{d} x \\quad(n=0,1,2, \\cdots), \\ b\_{n}=0 \\quad(n=1,2,3, \\cdots)\\end{array}\\right}\) 即知偶函数的傅里叶级数是只含常数项和余弦项的余弦级数\(\\frac{a\_{0}}{2}+\\sum\_{n=1}^{\\infty} a\_{n} \\cos n x\)

一般周期的傅里叶级数

\(2\\pi\)周期的傅里叶级数可以很容易推广到一般周期（设周期为\(T= 2l\)）：

定理 设周期为 2l 的周期函数 \(f(x)\) 满足收敛定理的条件,则它的傅里叶级 数展开式为\(f(x)=\\frac{a\_{0}}{2}+\\sum\_{n=1}^{\\infty}\\left(a\_{n} \\cos \\frac{n \\pi x}{l}+b\_{n} \\sin \\frac{n \\pi x}{l}\\right)(x \\in C)\)，其中： \(\\begin{aligned} a\_{n} \&=\\frac{1}{l} \\int\_{-1}^{1} f(x) \\cos \\frac{n \\pi x}{l} \\mathrm{d} x \\quad(n=0,1,2, \\cdots) \\ b\_{n} \&=\\frac{1}{l} \\int\_{-1}^{1} f(x) \\sin \\frac{n \\pi x}{l} \\mathrm{d} x \\quad(n=1,2,3, \\cdots) \\ C \&=\\left{x \\mid f(x)=\\frac{1}{2}\\left\[f\\left(x^{-}\\right)+f\\left(x^{+}\\right)\\right\]\\right} \\end{aligned}\) 当 \(f(x)\) 为奇函数时，\(f(x)=\\sum\_{n=1}^{\\infty} b\_{n} \\sin \\frac{n \\pi x}{l} \\quad(x \\in C)\)，其中\(b\_{n}=\\frac{2}{l} \\int\_{0}^{l} f(x) \\sin \\frac{n \\pi x}{l} \\mathrm{d} x \\quad(n=1,2,3, \\cdots)\) 当 \(f(x)\) 为偶函数时，\(f(x)=\\frac{a\_{0}}{2}+\\sum\_{n=1}^{\\infty} a\_{n} \\cos \\frac{n \\pi x}{l}(x \\in C)\)，其中\(a\_{n}=\\frac{2}{l} \\int\_{0}^{l} f(x) \\cos \\frac{n \\pi x}{l} \\mathrm{d} x \\quad(n=0,1,2, \\cdots)\)

傅里叶级数的复数形式

利用欧拉公式的如下形式：\(\\cos t=\\frac{\\mathrm{e}^{t \\mathrm{i}}+\\mathrm{e}^{-t\_{i}}}{2}, \\sin t=\\frac{\\mathrm{e}^{t\\mathrm{i}}-\\mathrm{e}^{-t\\mathrm{i}}}{2 \\mathrm{i}}\) 可将一般一般周期（设周期为\(T= 2l\)）的傅里叶级数华化为更简洁的复数形式：\(\\sum\_{n=-\\infty}^{\\infty} c\_{n} e^{\\frac{n \\pi x}{l} i}\) 其中\(c\_{n}=\\frac{1}{2 l} \\int\_{-l}^{l} f(x) \\mathrm{e}^{-\\frac{n \\pi x}{l} \\mathrm{i}} \\mathrm{d} x \\quad(n=0,\\pm 1,\\pm 2, \\cdots)\)

（推导过程详见高数同济第七版（下））

复数项级数

复数项级数定义

\(\\left(u\_{1}+v\_{1} \\mathrm{i}\\right)+\\left(u\_{2}+v\_{2} \\mathrm{i}\\right)+\\cdots+\\left(u\_{n}+v\_{n} \\mathrm{i}\\right)+\\cdots\)，其中\(u\_{n}\) 与 \(v\_{n}(n=1,2,3, \\cdots)\) 为实常数或实函数，这样的级数称为复数项级数。

复数项级数收敛定义

如果实部所成级数\(u\_{1}+u\_{2}+\\cdots+u\_{n}+\\cdots\)收敛于和u，虚部所成级数\(v\_{1}+v\_{2}+\\cdots+v\_{n}+\\cdots\)收敛于和v，则称复数项级数\(\\left(u\_{1}+v\_{1} \\mathrm{i}\\right)+\\left(u\_{2}+v\_{2} \\mathrm{i}\\right)+\\cdots+\\left(u\_{n}+v\_{n} \\mathrm{i}\\right)+\\cdots\)收敛，且其和为\(u+v i\)

复数项级数绝对收敛定义

如果复数项级数各项的模成的级数\(\\sqrt{u\_{1}^{2}+v\_{1}^{2}}+\\sqrt{u\_{2}^{2}+v\_{2}^{2}}+\\cdots+\\sqrt{u\_{n}^{2}+v\_{n}^{2}}+\\cdots\)收敛，称复数项级数绝对收敛。