高等数学-一元积分学-定积分的应用
几何应用
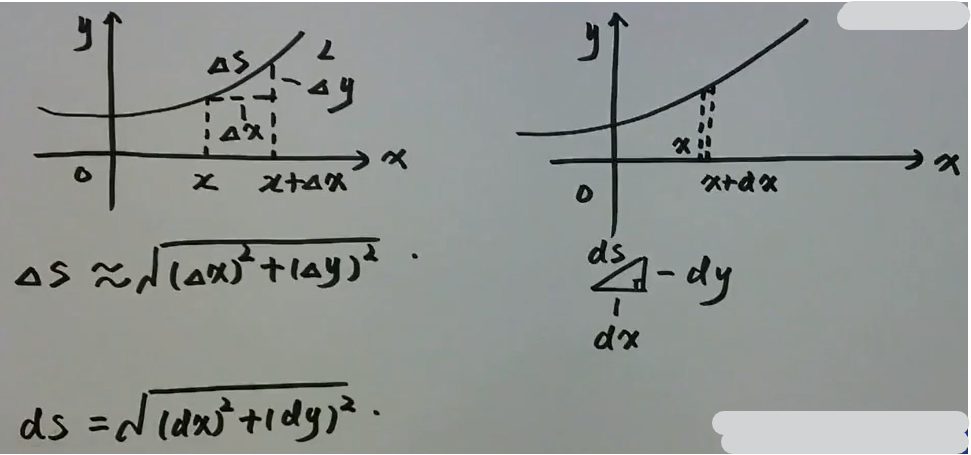
面积
直角坐标系中\(L : y=f(x) \\geqslant 0 \\quad(a \\leq x \\leq b)\)
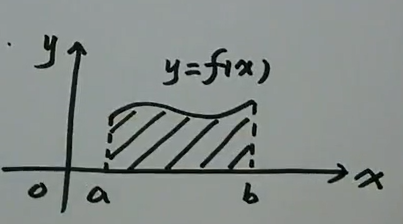
\(A=\\int\_{a}^{b} f(x) d x\)
极坐标系中\(L: r=r(\\theta) \\quad(\\alpha \\leq 0 \\leq \\beta)\)

取\(\[\\theta,\\theta+d \\theta\] \\subset\[\\alpha, \\beta\]\), \(d A=\\frac{1}{2} r^{2}(\\theta) d \\theta\) \(A=\\frac{1}{2} \\int\_{\\alpha}^{\\beta} r^{2}(\\theta) d \\theta\)

\(A=\\frac{1}{2} \\int\_{\\alpha}^{\\beta}\\left\[r\_{2}^{2}(\\theta)-r\_{1}^{2}(\\theta)\\right\] d \\theta\)
旋转体表面积

取\(\[x, x+d x\]\<\[a, b\]\), \(d A=2 \\pi | f(x) | \\cdot d s\) \(2 \\pi \\cdot | f(x) | \\cdot \\sqrt{\\left.1+f^{\\prime} | x\\right)} d x\) \(A=2 \\pi \\int\_{a}^{b}|f(x)| \\cdot \\sqrt{1+f^{\\prime}(x)} d x\)
体积
图形绕x轴旋转体积

取\(\[x, x+d x\]\<\[a, b\]\), \(d v=\\pi f^{2} (x) \\cdot d x\) \(V\_{x}=\\pi \\int\_{a}^{b} f^{2} (x) d x\)
图形绕y轴旋转体积

取\(\[x, x+d x\]\<\[a, b\]\), \(d v=2 \\pi|x| \\cdot|f(x)| \\cdot d x\) \(V\_{y}=2 \\pi \\int\_{a}^{b}|x| \\cdot|f(x)| \\cdot d x\)
已知截面面积求体积
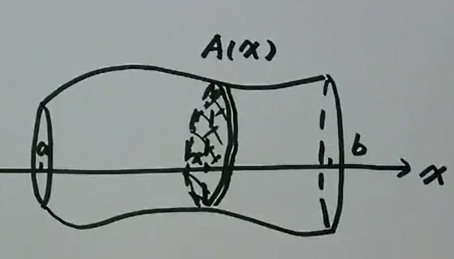
取\(\[x, x+d x\]\<\[a, b\]\), \(d v=A(x) d x\) \(v=\\int\_{a}^{b} A(x) d x\)
弧长
弧长部分可结合高等数学-一元微分学-应用-弧微分与曲率部分来看

直角坐标系\(L: y=f(x)(a \\leq x \\leq b)\)
取\(\[x, x+d x\]\<\[a, b\]\), \(d s=\\sqrt{1+f^{\\prime}(x)} d x\) \(l=\\int\_{a}^{b} \\sqrt{1+f^{\\prime 2}(x)} d x\)
参数方程\(\\begin{array}{l}\\left{\\begin{array}{ll}x=\\varphi(t) \\ y=\\psi(t)\\end{array}\\right. \& (\\alpha \\leqslant t \\leqslant \\beta)\\end{array}\)
取\(\[t, t+d t\]\<\[\\alpha , \\beta\]\), \(\\begin{aligned} d s \&=\\sqrt{(d x)^{2}+\\left( d y\\right)^{2}}=\\sqrt{\\left(\\frac{d x}{d t}\\right)^{2}+\\left(\\frac{d y}{d t}\\right)^{2}} d t \\ \&=\\sqrt{\\varphi^{\\prime}(t)+\\psi^{\\prime}(t)} d t \\end{aligned}\) \(l=\\int\_{\\alpha}^{\\beta} \\sqrt{\\varphi^{\\prime 2}(t)+\\psi^{\\prime 2} ( t)} d t\)
极坐标系\(L: r=r(\\theta)\)
极坐标曲线 \(r=r(\\theta), \\alpha \\leqslant \\theta \\leqslant \\beta\) 的弧长(其中 \(r(\\theta), r^{\\prime}(\\theta)\) 连续,且不同时为零) \[
s=\\int\_{a}^{\\beta} \\sqrt{r^{2}(\\theta)+r^{\\prime 2}(\\theta)} \\mathrm{d} \\theta
\]
圆\((a\>0)\)
\(x^{2}+y^{2}=a^{2} \\Leftrightarrow r=a\)
\(x^{2}+y^{2}=2 a x \\Leftrightarrow(x-a)^{2}+y^{2}=a^{2}\)对应极坐标系\(x=2 a \\cos \\theta\)
\(x^{2}+y^{2}=2 a y \\Leftrightarrow x^{2}+(y-a)^{2}=a^{2}\)对应极坐标系\(r=2 a \\sin \\theta\)
双扭线

\(\\left(x^{2}+y^{2}\\right)^{2}=a^{2}\\left(x^{2}-y^{2}\\right)\)对应极坐标系\(r^{2}=a^{2} \\cos 2 \\theta\)
摆线

\(L : \\left{\\begin{array}{l}x=a(t-\\sin t) \\ y=a(1-\\cos t)\\end{array} \\quad(0 \\leq t \\leq 2 \\pi)\\right.\)
心形线
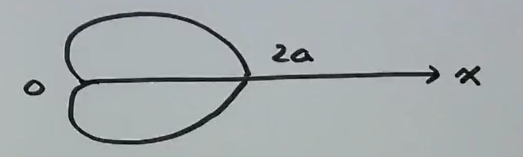
\(L: r=a(1+\\cos \\theta)\)
发表回复